| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Work | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Work of a Constant Force |
||
 Work of a Constant Force |
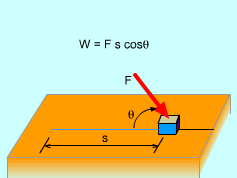
In physics, a constant force F does work when it undergoes a displacement in the direction of the force. If an object moves a distance s under this force, the work done by the force is given by the dot product of force and displacement vectors. W = F • s If the angle between the force and the moving direction is θ, then the equation can be written in scalar forma W = F s cosθ |
|
| Work of a Variable Force |
||
|
|
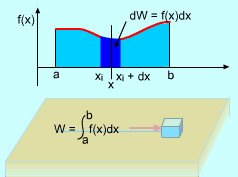
If the force F is not a constant, the work done by this force can be derived using integration over the path. Suppose an object moves along the x-axis in the positive direction from x = a to x = b. At each point between a and b a force f(x) acts on the object, where f is a continuous function. First divide [a, b] into n small subintervals, so the typical interval is [xi, xi + dx]. Let xi* be a point in this interval. The force at this point will be f(xi*). When this object moves from xi to xi+ dx, the work done by force f(x) can be approximated as dW = f(xi*) dx Using Riemann sum, the total work done by f(x) from x = a to x = b can be approximated as This approximation becomes better as n becomes larger. The work done
in moving the object from a to b is defined as the limiting value of this quantity as n approaches infinite, and it is a
definite integral: If the force and the moving direction has an angle θ, the work done by the force is |
|