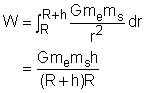| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Work | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
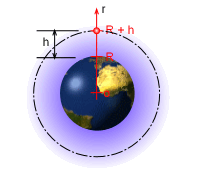
The work required to place a satellite into orbit needs to be determined. According to the Newton's Law of Gravitation, the attractive force between the earth and the satellite is: FG = Gmems/r2 where r is pointed from the center of the earth to the satellite. Since
r changes with the location of the satellite (from R, the average radius
of the earth, to (R + h), the sum of the earth's radius and the altitude
of the satellite), integration needs to be used to calculate the work. |
|
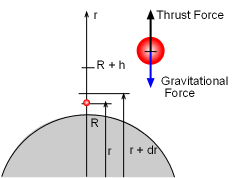 Work done between r and r + dr |
First, take an arbitrary location, r, on
[R, R + h], as shown
on the left. The force applied to overcome the gravitational force
is the same as the attractive force between the earth and the satellite
at that location. When the satellite moves from r to r + dr, work done by this force is dW = Fdr = Gm1m2/r2 dr Move the satellite from the earth surface ( r = R) to its orbit ( r = R + h) equals Substituting the given value into the above equation gives R + h = 6.37 x 106 + 650 x 103 = 7.02 x 106 m W = 6.67 x 10-11(5.98
x 1024)(173)(650
x 103) To move the satellite vertically to its orbit, requires 1,003 MW of work. This does not include work needed to move the rocket used to launch the satellite. |
|