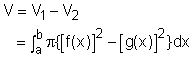| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Volume | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
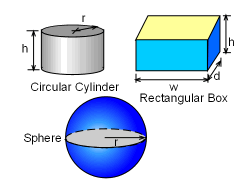 Circular Cylinder, Rectangular Box and Sphere |
In analytical geometry, the formula to calculate the volume of a circular cylinder, rectangular box and sphere were found to be:
In this section, the formula to calculate the volume of a solid of revolution and a cylindrical shell are introduced. |
|
| Definition of Volume |
||
|
|
|
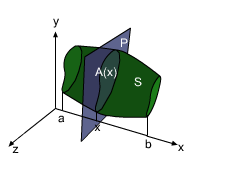
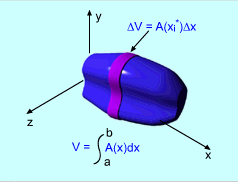
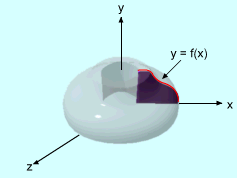
Before the volume of a sold of revolution can be calculated, some terms and regions need to be defined. The intersection of any body S with a plane P is a plane region called a cross-section of S. If P is perpendicular to the x-axis and passes through the point x on the x-axis, the area of the cross-section region is A(x), where x on the interval [a, b]. The area A(x) will very as x increases from a to b. Generally, it is easier to find the volume of a small uniform region and then sum them together to get the total volume. First, divide the interval [a, b] into n subintervals. Δx = (b - a)/n In each subinterval, choose a point xi*. On each subinterval [xi, xi+1], the volume can be approximated as a volume of a disk which has a face area of A(xi*) and height Δx. Vi = A(xi*)Δx Then the volume of the region where x is on interval [a, b] can be approximated as If A(x) is continuous, the limit of the above Rieman sum exits. The exact volume is given by In a similar way, a cross-section area can be generated about y-axis using A(y) where y is in an interval [c, d]. The volume is given by |
| Volumes of Solids of Revolution |
||
|
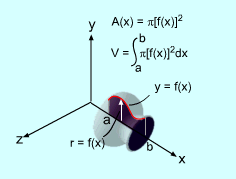
A solid of revolution is obtained by revolving a region in a plane about a line that does not intersect the region. The line about which the rotation takes place is called the axis of revolution. Considering a curve defined by a function, y = f(x), where x is on an interval [a, b]. Rotate the region bounded by the curves y = f(x), y = 0, x = a, and x = b about x-axis. Then a solid body S is generated. Because S is obtained by rotation, a cross-section through x on the x-axis perpendicular to the x-axis is a circular disk with radius and the cross-sectional area of the circular disk is A(x) = πy2 = π[f(x)]2 Using the basic volume formula derived above, the formula for a volume of revolution is |
|
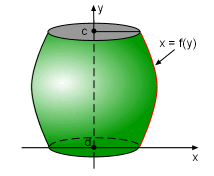 Volume of Revolution by x = f(y) |
In a similar way, if rotate a curve defined by a function x = g(y), where y is on an interval [c,d], the volume of this revolution is |
|
|
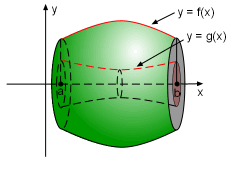
If rotating a region bounded by the curves y = f(x), y = g(x), x = a, and x = b about the x-axis, a solid body with a "hole" in the middle S is generated. The volume of this body can be obtained by subtracting volumes shown below. If V1 is the volume of the revolution by rotating the curve y = f(x), where x is on an interval [a, b] and V2 is the corresponding volume for the curve y = g(x), where x is on an interval [a, b], the volume of S is calculated by subtracting V2 from V1 |
|
| Volumes by Cylindrical Shells |
||
|
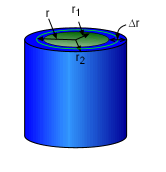
Some volume problems are difficult to handle using the method of revolution. Another method called cylindrical shells can be easier in these cases. First consider a cylindrical shell with inner radius r1 and outer radius r2, and height h. The volume V is calculated by subtracting the volume of the inner cylinder from the volume of the outer cylinder. V = (π r22h - π r12h) = 2π(r2 + r1)/2h(r2 - r1) = 2πrhΔr where r = (r2 + r1)/2 is the average radius of the shell, Δr = r2 - r1 is the thickness of the shell, and 2πr is the average circumference of the face of the shell. Then consider a solid body obtained by rotating about the y-axis the
region bounded by y = f(x) Δx = (b - a)/n Choose a value, xi* in the middle of each subinterval, then the volume corresponding to f(x) between [xi, xi+1] can be approximated as a cylindrical shell with a height of f(xi*), a thickness of Δx, and an average radius xi* = (xi + xi+1)/2. Vi = 2πxi* f(xi*)Δx An approximation to the volume V of S is given by the sum of the volumes of these shells The exact volume is obtained when n approach infinity in the above expression. |
|