| Ch 9. Friction | Multimedia Engineering Statics | ||||||
| Friction I | Friction II | ||||||
| Friction II | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| STATICS- Example |
||
| Example |
||
|
|
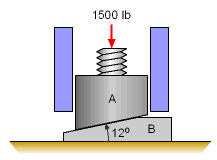
The vertical position of a machine (block A) is adjusted by moving wedge B. The coefficient of static friction between all surfaces is 0.3. Determine the horizontal force, P, acting on wedge B, that is required to a) raise the block A (acting on the right side), and |
|
| Assume the weight of blocks A and B are small. | ||
| Solution (a) - Load P to Raise Block A |
||
 Raising the Machine |
The first part of this problem asks for the the smallest value of the force, P, to raise the machine. This force will act on the right side of the wide of block A, as shown, in order to push block A upward. As with all static problems, a free-body diagram will help identify all forces acting on an object. Since there is a known force of 1,500 lb acting on block A, this object will be analyzed first. All forces acting on the block 'A' are shown in the free-body diagram on the left. The frictional forces are, |
|
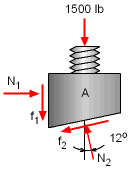 Free-body Diagram of Block A |
f1 = μ N1 = 0.3 N1 Applying the equilibrium equations gives, ΣFx = 0 ΣFy = 0 Solving above two equations gives, N2 = 1,960 lb and the frictional forces are, f2 = 587.9 lb | |
 Free-body Diagram of Block B |
Now that the forces on the bottom surface of block A are known, wedge B can be analyzed. First, sum the forces in the vertical direction, to give, ΣFy = 0 Finally, P can be determined by summing forces on wedge B in the horizontal, ΣFx = 0 P = 1,521 lb | |
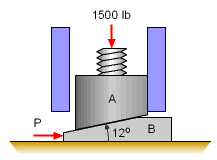 Lowering the Machine |
Solution (b) - Load P to Lower Block A |
|
The second part of this problem asks for the the smallest value of the force, P, to lower the machine. This force will act on the left side of the wide of block A, as shown, in order to lower block A downward. Since force P is acting in the opposite direction than in the previous solution, the forces acting on block A will be in opposite directions. The new forces acting on the block A are shown in the free-body diagram on the left. Frictional forces are given by, |
||
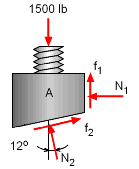 Free-body Diagram of Block A |
f1 = μ N1 = 0.3 N1 Applying the equilibrium equations gives, ΣFx = 0 ΣFy = 0 Solving above two equations gives, N1 = 120.1 lb and the frictional forces are, f1 = 36.03 lb |
|
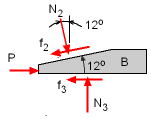 Free-body Diagram of Block B |
Now that the forces on the bottom surface of Wedge A are known, wedge B can be analyzed. First, sum the forces in the vertical direction, to give, ΣFy = 0
Finally, P can be determined by summing forces on wedge B in the horizontal, ΣFx = 0 P = -559.5 lb |
|
| Comments | ||
| To keep the machine in equilibrium one should apply a force of magnitude greater then 559.5 lb in ← direction but less than 1,521 lb in the same direction. If the applied force is more than 1,521 lb, the machine will be raised and if applied force is less than 559.5 lb then the machine will be lowered due to it's own weight. | ||