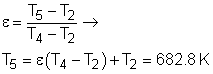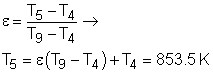| Ch 9. Brayton Cycle | Multimedia Engineering Thermodynamics | ||||||
|
Brayton Cycle |
Intercooling and Reheating |
||||||
| Brayton Cycle with Intercooling | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||
|
Several suggestions are given to modify a power plant. The power output and thermal efficiency of each plan need to be determined. Assumptions:
|
||||||||||||||||||||||
|
|
The network output from a cycle can be determined by the energy balance of the cycle. It is wnet,out = qin - qout And the thermal efficiency of a cycle can be determined by its general definition. ηth,Brayton =1
- qout /qin |
|||||||||||||||||||||
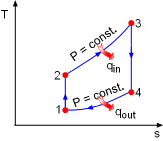 T-s Diagram of the Simple Ideal Brayton Cycle |
(1) Determine the net work output and the thermal efficiency of the simple ideal Brayton cycle The T-s diagram of the simple ideal Brayton cycle is shown on the left. Under the cold-air-standard assumption, heat input equals the enthalpy difference in the constant-pressure heat addition process. Likewise, heat output equals the enthalpy difference in the constant-pressure heat rejection process. qin = h3 - h2 = cP(T3 - T2) qout = h4 - h1 = cP(T4 - T1) Therefore, temperature at each state in the cycle needs to be determined first. T1 = 300 K (given) 1-2: Isentropic compression: 2-3: Constant pressure heat addition: 4-1: Constant pressure heat rejection: 3-4: Isentropic expansion: After determining all the temperatures, the heat input and heat rejection can be calculated. qin = cP(T3 -
T2) Net work output and thermal efficiency of this cycle can be determined with qin and qout. wnet,out = qin -
qout = 760.3 - 419.7 = 340.6 kJ/kg |
|||||||||||||||||||||
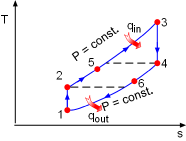 T-s Diagram of the Ideal Brayton Cycle withRegeneration |
(2) Determine the net work output and the thermal efficiency of the ideal Brayton cycle with regeneration The T-s diagram of the ideal Brayton cycle with regeneration is shown on the left. Heat input and heat output in this cycle are: qin = h3 - h5 = cP(T3 - T5) qout = h6 - h1 = cP(T6- T1) Temperatures of state 1, 2, 3, and 4 can be determined by the same way as the simple ideal Brayton cycle and they are the same as in (1). 2-5: constant pressure regeneration: 4-6: constant pressure regeneration: The energy balance in the regenerator is: h5 - h2 = h4 - h6 Under cold-air-standard assumption, the temperature at state 6 is T6 = T4 - (T5 - T2) = 578.3 K Substituting the temperatures into the expression of qinand qout gives qin = cP(T3 -
T5) qout = cP(T6-
T1) Net work output and thermal efficiency of this cycle can be determined as wnet,out = qin - qout = 620.3 - 279.6
= 340.6 kJ/kg |
|||||||||||||||||||||
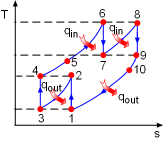 T-s Diagram of the Ideal Brayton Cycle with Intercooling, Reheating and Regeneration |
(3) Determine the net work output and the thermal efficiency of the ideal Brayton cycle with intercooling, reheating and regeneration The T-s diagram of the ideal Brayton cycle with intercooling, reheating, and regeneration is shown on the left. Under the cold-air-standard assumption, heat input is the sum of the enthalpy differences in the constant-pressure heat addition process and the reheating process. Heat output equals the sum of the enthalpy differences in the constant-pressure heat rejection process and the intercooling process. qin = (h6 - h5) + (h8 -
h7) qout = (h10 -
h1) + (h2 - h3) The temperature at each state can be determined by the same way as in (1) and (2). T1 = 300 K (given) For optimum operation, equal pressure ratios are maintained across each state. The total pressure ratio is given as rP = 8 P2 = 2.828P1= 282.8 kPa 1-2: isentropic compression: 2-3: constant pressure intercooling. For optimum operation, air is cooled to a temperature same as the temperature at the compressor inlet. Hence, T3 = T1 = 300 K 3-4: isentropic compression: P4 = 2.828P3 =
800 kPa Temperature at state 6 reaches the maximum value. The temperature is given as T6 = 1,300 K 4-5-6: constant pressure process: P6 = P4 = 800 kPa 6-7: isentropic expansion: P7 = P6 /2.828 = 282.8 kPa 7-8: constant pressure reheating process: P8 = P7 = 282.8 kPa For optimum operation, air is heated to the same temperature at each inlet of the turbine. Hence, T8 = T6 = 1,300 K 9-10-1: constant pressure process: P9 = P1 = 100 kPa 8-9: isentropic expansion: 4-5 and 9-10: constant pressure regeneration: |
|||||||||||||||||||||
The regeneration has an effectiveness ε = 0.8
The energy balance in the regenerator is: h5 - h4 = h9 - h10 Under cold-air-standard assumption, the temperature at state 10 is T10 = T9 - (T5 - T4) = 516.2 K Substitute the temperatures into the expression of qin qin = cP(T6- T5) + cP(T8-
T7) qout = cP(T10- T1) + cP(T2-
T3) After determining qin and qout, the net work output and the thermal efficiency of this cycle can be calculated. wnet,out = qin - qout = 784.5 -
321.6 = 463.0 kJ/kg |
||||||||||||||||||||||
(4) Results analysis The heat input, heat output, net work output, and thermal efficiency
of all three cycles are summarized in the following table. |
||||||||||||||||||||||
|
||||||||||||||||||||||
| Among the three cycles discussed above, the simple Brayton cycle has the lowest thermal efficiency and the smaller work output. Compared with the simple Brayton cycle, Brayton cycle with regeneration can produce the same work with less heat input. Brayton cycle with intercooling, reheating, and regeneration has the highest thermal efficiency and larger work output. Also, it consumes more fuel due to reheating compared with the other two cycles. | ||||||||||||||||||||||