| Ch 9. Friction | Multimedia Engineering Statics | ||||||
| Friction I | Friction II | ||||||
| Friction II | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
|
|
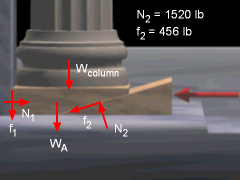
The solution requires finding the smallest magnitude of P required to move the column. First, consider the forces acting on wedge A. Force equilibrium provides two equations, ΣFx = 0 ΣFy = 0 Since motion is impending, the friction forces are f1 = μ N1 = 0.3 N1 If these two friction equations are used, the four equations can be reduced to two equations and two unknowns, N1 and N2. N1 - 0.3 N2 cos15 - N2 sin15 = 0 N1 = 0.5486 N2 Solving gives N2 = 1,520 lb and N1 = 833.3 lb and the friction forces are f2 = 456.0 lb and f1 = 250.0 lb |
|
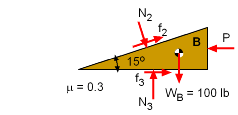 Free Body Diagram for Wedge B |
Now that the forces on the bottom surface of Wedge A are known, wedge B can be analyzed. First, sum the forces in the vertical direction, to give, ΣFy = 0 N3 = 1,450 lb and f3 = 435 lb Finally, P can be determined by summing forces on wedge B in the horizontal, ΣFx = 0 Solving for P gives, P = 1,269 lb |
|
| Solution of b) |
||
|
|
The applied force and lateral constraints have been removed. As a result, the direction of potential motion has changed, and the frictional forces will reverse direction. The equations of equilibrium on wedge A will produce ΣFx = 0 ΣFy = 0 Since the status of the wedge is being analyzed, it cannot be assumed that f2 = μN2. The resulting forces are N2 = 1,063 lb and f2 = 285 lb The friction due to impending motion is determined as f2 max = μ N2 = 318.9 lb Since this value is greater than the friction due to equilibrium, wedge A must be in equilibrium. The minimum coefficient of friction value required to maintain equilibrium is 0.268. Since the top wedge is not moving, it is impossible for the bottom wedge to move. This can be verified with a free-body diagram of wedge B. Also, if the column force were to increase due to the weight from the ceiling, the wedge would still not move. Feel free to experiment with this and other factors in the simulation. |
|