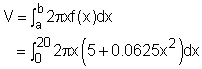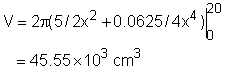| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Volume | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
A mold is constructed by rotating clay in a cylindrical container. The angular velocity and the volume of clay need to be determined. |
||
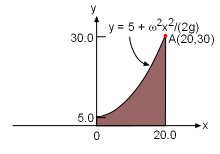 Curve go through (20, 30) |
1. The angular velocity y = 5 + ω2x2 /(2g) The curve must go through point A, so substitute x = 20 and y = 30 ,
into the function gives the angular velocity. Notice g = 980.7 cm/s2 Substitute ω into the curve function gives y = 5 + 0.0625x2 |
|
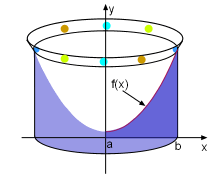 Generating the Volume by Rotating the Shadow Region about y-axis |
2. The volume of the clay The volume is generated by rotating the shadow region on the left around y-axis, which generate a cylindrical shell. The volume of a cylindrical shell is given as 45,550 cm3 clay is needed to build this mold. |
|