In previous sections, it was assumed that objects were frictionless. Consequently, the only reaction forces were normal to the surface. This ideal approximation always involves relative errors because no surface is perfectly frictionless.

There are several types of frictional forces used in mechanics. However, dry friction will be the primary form considered in this section.

Mechanics of Friction

Friction vs Force

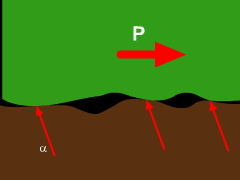
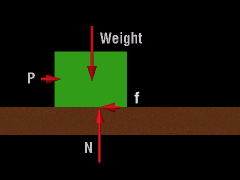
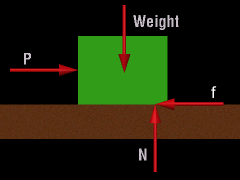
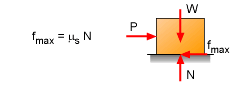
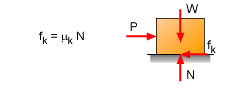
Dry friction, also known as Coulomb friction, occurs between two rough, solid surfaces.

Frictional forces always oppose the tendency towards motion and act tangential to the surfaces in contact.

Static friction describes surfaces that are in contact but not moving. The maximum static friction is represented by

     f_max = μ_s N

Here, μ_s is a proportionality constant called the coefficient of static friction. This equation only gives the force of friction when motion is impending. If motion is not impending, then the friction force, f_s, will be less than the maximum, or

     f_s ≤ μ_s N

Thus, only when motion is just starting to take place will the friction force be a maximum.

On the other hand, if motion has started, then kinetic friction is used, or

     f_k = μ_k N

Here, μ_k is the coefficient of kinetic friction. This equation only applies when an object is in motion. It is generally true that μ_k is less than μ_s and may vary slightly with velocity. In general, friction simply written as

     f = μ N

It is also helpful to consider the resultant of the frictional and normal forces. The angle α from the normal force to the resultant can be calculated as

     tanα = f/N = μ

As the static friction approaches f_max, α reaches a maximum angle φ_s.

     tanφ_s = μ_s

Likewise, a similar equation for kinetic friction can be written as

     tanφ_k = f_k/N = μ_k

The angles φ_s and φ_k define the limiting positions of the reactions between surfaces. There are typically three types of friction problems.

Impending motion is known to exist because the system is on the verge of slipping. The equilibrium equations and basic equation F_max = μ_s N hold true.

Neither impending motion nor motion is known. Using equilibrium equations, the friction force direction on a surface is assumed and solved. Comparing the results give

1. f < (f_max = μ_s N) System is still in equilibrium.
2. f = (f_max = μ_s N) Motion is impending.
3. f > (f_max = μ_s N) This condition would violate equilibrium and therefore is impossible. Instead, it indicates that the system is in motion and maximum friction is μ_kN.

Relative motion exists between the surfaces. Therefore, the properties of kinetic friction would be in effect.