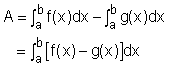| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Area Between Curves | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Areas between a Curve and the y Axis |
||
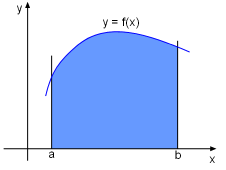 Area under Curve |
The definite integrals section has defined that the area under a curve of function y = f(x) between x = a and x = b equals the definite integral In this section, integrals are used to find areas between curves. |
|
| Areas between Curves |
||
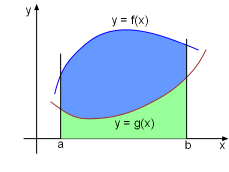
 Area between Two Curves |
Consider the region S, shown on the left,
lies between two curves y = f(x) and y = g(x), and between two vertical lines x = a and x =b, where f and g are continuous functions and f(x) To find the area of S, divide the interval [a, b] into n pieces. The width of each piece is Δx = (b-a)/n The left endpoint for a given sub-interval i is xi = a + idx in which i = 0, 1, 2, ..., n-1. |
|
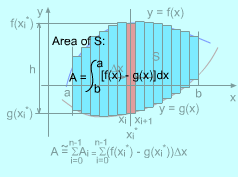 Area between Curve: Rectangle Approximate |
Consider a typical rectangle (red in the left diagram) between xi and xi+1, Choose a x in [xi, xi+1], say xi*, then the height of this typical rectangle is h = f(xi*) - g(xi*) The width of this typical rectangle is w = xi+1 - xi = Δx Then the area of this typical rectangle is ΔA = (f(xi*) - g(xi*))Δx The Rieman sum gives the approximate area of S. Since f and g are continuous, the limit of this Rieman sum exits. Therefore,
the area of the region bounded by the curves y = f(x) , y = g(x), and
the lines x = a and x = b, where f and g are continuous and and f(x ) |
|
|
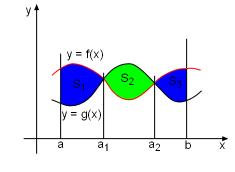
If both f and g are positive, the area between these two curves can be find out directly from the definite integral. A =[area under y = f(x)] - [area
under y =g(x)] A = A1+ A2 + ... Since The area between the curves y = f(x) and y = g(x) and between x =a and x =b is |
|
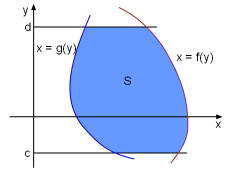 Area between Curve: x as a Function of y |
In some cases, the area between curves is easier to calculate if the function are in terms of y, instead of x. If a region S is bounded by curves x = f(y) and x = g(y), and lines y = c and y = d, where f and g are continuous, the area of S is
|
|