Example Graphic

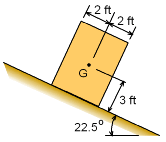
It is observed that when a flat bed of the dump truck is raised to an angle of 22.5^o, a box that was loaded on the bed begins to slide. Determine the static coefficient of friction between box and the surface of bed of dump truck. Also check if the box will tip before it slides. The box is 6 feet high and 4 feet wide and its center of gravity is at its center.

Simplified System Diagram

Free-body Diagram of the System

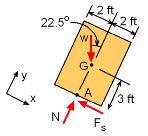
The problem can be simplified as a box slide down a hill as shown in the figure on the left. The center of gravity is 3 feet from the bottom.

There are three possible forces acting on the box, its weight, reaction force due to the ground and the friction force. The location and direction of these forces are shown on the free-body diagram of the box on the left. Let the resultant normal force, N be acting at point A. There are two unknowns, N and F_s.

Note that the co-ordinate system is rotated by 22.5^o in clockwise direction to simplify the calculations. For equilibrium,

     ΣF_y = 0
     N - w cos 22.5 = 0
     N = w cos 22.5

     ΣF_x = 0
     w sin 22.5 - F_s = 0

     F_s = μ N = μ w cos 22.5

     Putting back F_s in ΣF_x equation gives,

     w sin 22.5 = μ w cos 22.5
     μ = tan 22.5 = 0.4142

Notice from the calculation that static coefficient of friction, μ, is independent of the weight of a box. Also, knowing the inclination angle of the bed is a convenient way of measuring the coefficient of static friction.

Free-body Diagram of the System

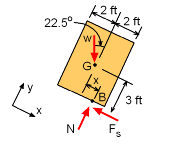
To check whether box will tip or slide first, let the resultant normal force, N be acting at point B which is at distance x as shown in the figure on the left.

Taking moments about point 'B' and assuming counter clockwise (CCW) moment as positive gives,

     ΣM_B = 0
     w (cos 22.5) x - w (sin 22.5) 3 = 0
     w (cos 22.5) x = w (sin 22.5) 3
     x = (tan 22.5) 3
     x = 1.243

'x' is less than 2 ft which means the box will slide before it can tip. Also notice from the calculation that distance 'x' is independent of the weight of a box but it does depend on the inclination angle and the distance between the center of gravity and the base.