| Ch 9. Friction | Multimedia Engineering Statics | ||||||
| Friction I | Friction II | ||||||
| Friction I | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
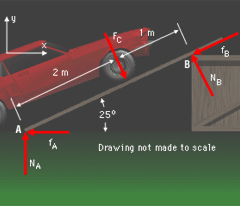
 Development of the Free Body Diagram
|
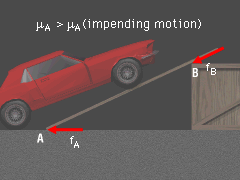
In this problem, the ramp AB may slide if the friction force at A is too low. To find the coefficient of friction that will prevent the ramp from sliding, the conditions under which the ramp will be in motion needs to be determined. First, draw a free-body diagram of the ramp with the friction acting to the left since the ramp will want to slide to the right. Using equilibrium equations, the moment about point A can be found as, ΣMA = NB (3 m) - FC (2 m) = 0 NB = (1,000 N) (2 m) / (3 m) = 666.7 N Since motion is impending at each point and the normal force at point B is known, the friction at point B is fB = μB NB = (0.2)(666.7 N) = 133.3 N The equilibrium equations can now be used to find the normal and frictional forces at point A. ΣFx = 0 fA = FC sinα - NB sinα - fB cosα
ΣFy = 0 NA = FC cosα - NB cosα - fB sinα
Now that the normal and frictional forces are known, the coefficient of friction can be determined as μA = fA/NA = 0.056 This is the lowest value of μA needed to prevent motion. For lower values of μA, the ramp is in motion, and for higher values, the ramp is in equilibrium. |
|