| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Area Between Curves | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
A police car at rest chases a passing car which has a velocity of 80 mph. The time required for the police car to catch the passing car needs to be determined. |
||
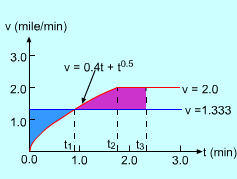 Velocity Functions of Both Cars |
The velocity function of both cars are shown
on the left. Transfer the unit of velocity to miles/minute to get better
graphics. Then the velocity of the passing car is 1.333 miles/minute , and the
police car's velocity function is Velocity is simply v = ds/dt, so the distance, s, can be determined as, Assume t1 is the time the police car's velocity reaches the velocity of the passing car (v = 1.333 mile/min), t2 is the time the police car's velocity reaches 120 mph (2 mile/min), and t3 is the time the police car reaches the passing car. |
|
Simplifying the above equation gives, First, t2 can be determined since the maximum velocity of the police car is known. v = 2.0 = 0.4t2 + t2
0.5 Next, integrate the equation and solve for t3 gives 1.333t2 - 0.2t22 -
2/3(t2)1.5 - 0.6667(t3 - t2)
= 0 The result shows the police car needs 2.016 minutes to catch the passing car. |
||