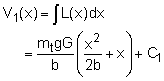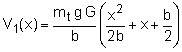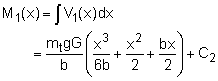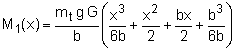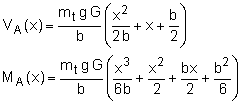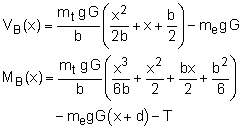STATICS - CASE STUDY SOLUTION
|
Loading on P38 Wing
|
|
The total solution can be found by determining the shear force distribution and bending moment distribution of the three separate types of loading (distributed lift, engine mass, and engine torque) and then combining them through the principle of superposition.
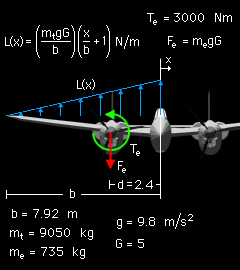
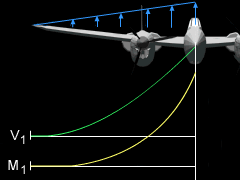
It is important to use the same x-coordinate system for each of the diagrams so that they can be superimposed. The lift distribution is given as an equation where x is positive from the the center of the aircraft, as shown in the diagram at the left. |
| |
|
| |
1. Distributed Lift
|
| |
The more difficult loading is the linear distribution loading due to the lift on the wing. The shear force distribution on the wing can be calculated by integrating the loading function, the lift distribution, from the left free end to any point, x, on the wing,
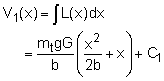
|
| |
|
|
Distributed Lift Load |
|
The integration constant, C1, can be determined by using the boundary condition that the shear force on the wing tip (x = -b) must be zero. Thus,
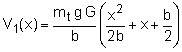
Similarly, the bending moment can be found by integrating the shear force distribution, as
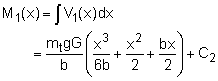
The bending moment force on the wing tip must be zero which is used to determine the integration constant. The moment function becomes,
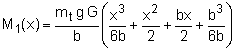 |
| |
|
|
| |
|
2. Engine Mass
|
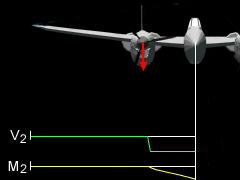
Engine Mass as Point Load |
|
Next, consider the shear and moment diagrams for the engine point force load. The shear force is zero up to the engine location, so
V2A(x) = 0 -b
≤ x ≤ -d
At the engine location, there is a jump in shear force due to the weight of the engine, giving
V2B(x) = -Fe = -me g G -d
≤ x ≤ 0
The bending moment distribution is found by integrating the shear force distribution in both sections, giving:
M2A(x) = 0 -b
≤ x ≤ -d
M2A(x) = -me g G x + C3
The integration constant can be determined by noting that the moment at x = -d must be zero (engine locations). This gives the final moment equation as
M2A(x) =
-me g G (x + d) -b ≤ x ≤ -d |
| |
|
|
| |
|
3. Engine Torque
|

Engine Torque Load |
|
The engine torque has no effect on the shear force so the shear equation is simply zero.
V3(x) = 0
The bending moment is zero up to the engine location:
M3A(x) = 0
At the engine location, there is a jump in bending moment due to the engine torque, giving
M3B(x) = -T
|
| |
|
|
| |
|
Total Solution
|
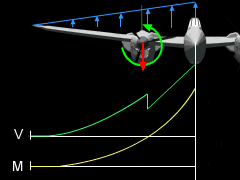
Total Solution from all Three Loaded |
|
The complete shear and moment diagrams can be constructed by adding the individual shear and moment equations.
From x = -b to x = -d, this gives
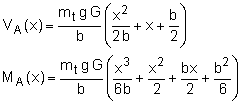
From x = -d to x = 0, the equations are
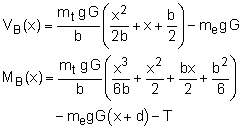
The critical points for the shear force and bending moment can now easily be located and evaluated.
|
| |
|
|
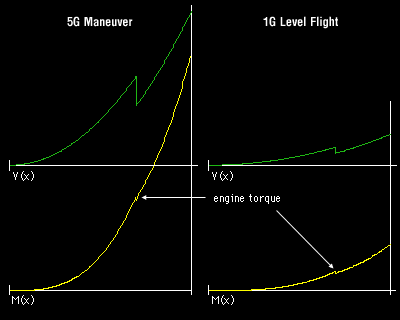
Expanded Diagrams for Loads |
| |
|
|