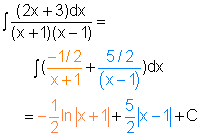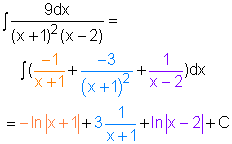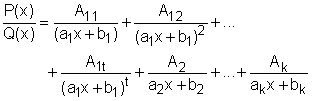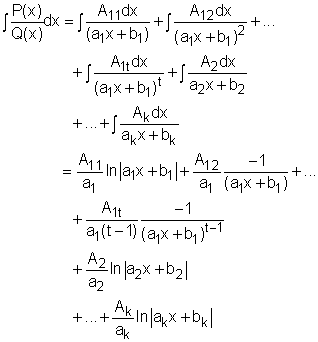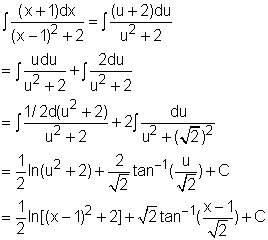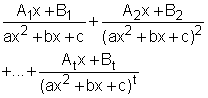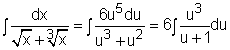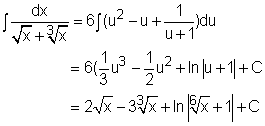| Ch 8. Integration Techniques | Multimedia Engineering Math | ||||||
|
Integration by Parts |
Trig. Integrals Trig. Subst. |
Fractions & Substitutions |
Approximate Integration |
||||
| Partial Fractions and Rationalizing Substitutions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||
This section introduces how to integrate a rational function (a ratio of polynomials) by expressing it as a sum of partial fractions, called partial fractions. |
|||
| Integration of Rational Functions |
|||
 A Proper Rational Function |
To see how the method of partial fractionsworks in general, consider a rational function f(x) = P(x)/Q(x) where P(x) and Q(x) are polynomials. Assume the degree of P(x) is less than the degree of Q(X) (called proper rational function). To integration this proper rational function, first express it as a sum of partial fractions of the form A/(ax + b)i or (Ax + B)/(ax2 + bx + c)j where A, B, a, b, and C are constant, and i, j are any positive integer.
There are four cases that occur. |
||
|
Case 1: The denominator Q(x) is a product of distinct linear factors Since the denominator Q(x) is a product of distinct linear factors, it can be written as Q(x) = (a1x + b1)(a2x + b2) ... (akx + bk) where no factor is repeated. In this case the proper rational function can be expressed as where A1, A2,..., Ak are constant. The following example shows how to determine these constants. Consider a proper rational function P(x)/Q(x) = (2x + 3)/(x2 - 1) Since x2 -1 = (x + 1)(x - 1), the partial fraction decomposition has the form Multiplying both sides of the above equation by (x + 1)(x - 1) gives, 2x + 3 = A1(x -1) + A2(x + 1) = (A1 + A2)x + (A2 - A1) The polynomials above are identical, so their coefficients must be equal. 2 = A1 + A2 Solving the above two equations gives A1 and A2. A1 = -1/2 and A2 = 5/2 Then the partial fraction of this proper rational function is Recall, the integration of Ak /(akx + bk) is where C is a Constant. Therefore, the integration of the proper rational function is where C is a Constant. |
||
|
Case 2: Q(x) is a product of linear factors, some of which are repeated. Suppose the first linear factor (a1x + b1) is repeated t times, then the proper rational function can be expressed as The constant A11, A12,..., A1t, A2, ..., Ak can be determined using the same way as case 1. Recall, the integration of A/(ax + b)rt, where r > 1, is Therefore, the integration of the proper rational function is,
|
||
Case 3: Q(x) contains irreducible quadratic factors, none of which are repeated. If Q(x) has a term ax2 + bx + c, where b2 - 4ac < 0, then in addition to case 1 and 2, the expression of P(x)/Q(x) will have a term of the form Ax+ B/(ax2 + bx + c) To integrate the above expression, (ax2 + bx + c) needs to be rewritten as the following form by completing the square. ax2 + bx + c = a(x+ d)2 + e and use the following formula The next example shows how to integrate Ax+ B/(ax2 + bx + c). Make the substitution u = x -1, then du = dx, and x = (u + 1). |
|||
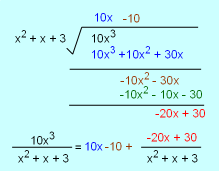 Preliminary Step of Dividing Q(x) by P(x) |
Case 4: Q(x) contains a repeated irreducible quadratic factor If Q(x) has a factor (ax2 + bx + c)t, where b2 - 4ac < 0, then the following terms will occur in the partial decomposition of P(x)/Q(x). and each term in the above equation can be integrated by completing the square and making a tangent substitution, as shown in case 3. The above methods work for proper rational functions. If the rational function P(x)/Q(x) is improper, which means the degree of P(x) is large than the degree of Q(x), the preliminary step of dividing Q(x) by P(x) until a remainder R(x) is obtained such that the degree of R(x) is smaller than Q(x). Then R(x)/Q(x) is a proper rational function and the above method can be used. The example on the left gives how to do the preliminary step of dividing. |
||
| Rationalizing Substitutions |
|||
Some functions can be changed into rational
functions by substitutions and therefore integrated by the above method.
When the integrand contains
an expression of the form In order to find the integration of This substitution changes the integrand to an improper rational function. The preliminary step of dividing (u + 1) by u3 gives The function 1/(u +1) is a simple proper rational function with P(u) =1 and Q(u) = u+1. where C is a constant. |
|||