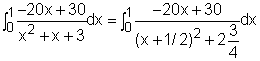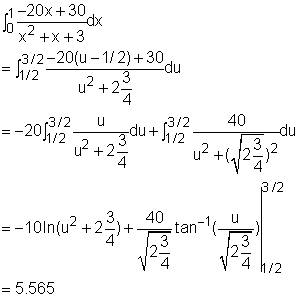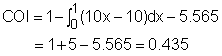| Ch 8. Integration Techniques | Multimedia Engineering Math | ||||||
|
Integration by Parts |
Trig. Integrals Trig. Subst. |
Fractions & Substitutions |
Approximate Integration |
||||
| Partial Fractions and Rationalizing Substitutions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
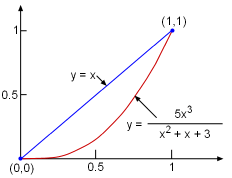
A given Lorenz curve is used to represent the income distribution of a country. The coefficient of inequality for this Lorenz curve needs to be determined. |
||
|
|
The coefficient of inequality is defined as where L(x) is the equation of the Lorenz curve, which is given as L(x) = 5x3/(x2 + x +3) Therefore, the coefficient of inequality equals the following integration. |
|
|
|
The second term of the above expression is an integration of an improper rational function.The first step is to simplify it to a proper ration function by the dividing (x2 + x + 3) by 10x3 (steps are shown on the left). Then the COI becomes, The last term of the above expression is a proper rational function. Since (x2 + x + 3) is an irreducible quadratic factor, it can be integrated by completing the square and making a tangent substitution. Make the substitution u = x +1/2, then du = dx, x = u - 1/2 Substitute the value into equation (1) gives the COI The coefficient of inequality equals 0.435. |
|

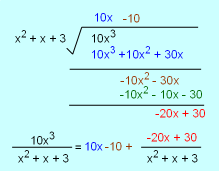
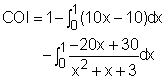 (1)
(1)