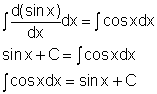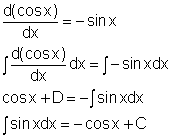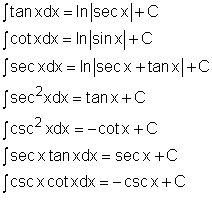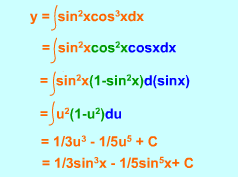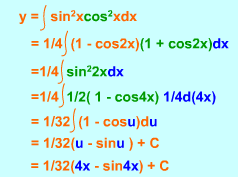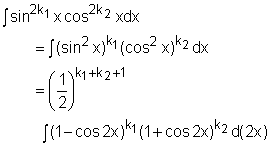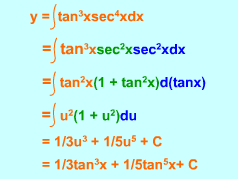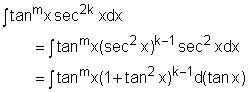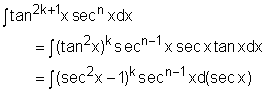| Ch 8. Integration Techniques | Multimedia Engineering Math | ||||||
|
Integration by Parts |
Trig. Integrals Trig. Subst. |
Fractions & Substitutions |
Approximate Integration |
||||
| Trigonometric Integrals and Trigonometric Substitutions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
|
This section will examine integration of trigonometric functions using basic trigonometric identities. Also, three types of trigonometric substitutions are introduced to help integrate complex trigonometric functions. To start, the basic sine and cosine functions need to be integrated. In a previous section, the derivatives of trigonometric functions were introduced. For example, d(sinx)/dx = cosx Integrating both side of the above equation gives, The above equation means the integral of cosine is sine. In the similar way, the integral of sine is negative cosine. Similarly, other basic trigonometric functions can also be integrated to give: |
|
| Complex Trigonometric Integrals |
||
|
The above basic trigonometric identities are used to integrate certain combinations of trigonometric functions. The first type of combinations of trigonometric functions is powers of sine and cosine. Form 1: The following general strategy is used in
evaluating integrals of the form
|
|
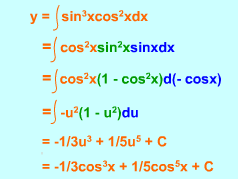 Integration of sin3x cos2x |
|
|
|
|
|
|
The second type of combinations of trigonometric functions is powers of tangent and secant. Form 2:
|
|
 Integration of tan3x sec3x |
|
|
 Integration of sin2x cos3x |
The third type of combinations of trigonometric functions is production of sine and cosine. Form 3: The following identities are used to evaluate the integrals have form 3.
|
|
| Trigonometric Substitutions |
||
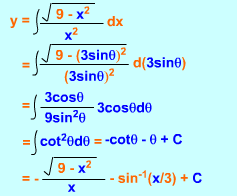 Integration of sin2x cos3x |
When an integral of the form Type 1: If Type 2: If Type 3: If |
|