| Ch 8. Incompressible and Viscous Flow | Multimedia Engineering Fluids | ||||||
|
Flow between Parallel Plates |
Couette Flow |
Viscous Flow in Pipe |
|||||
| Couette Flow | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
In another section, analytical solutions were obtained for flow between fixed parallel plates. In this section, the parallel plates are no longer fixed, and can be moved at a given velocity. This type of problem is generally referred as Couette flow. |
||
| Couette Flow |
||
|
|
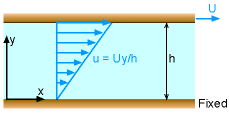
Consider flow between parallel plates, as shown in the figure where the top plate moves at a velocity U. The general velocity profile can be obtained from the Navier-Stokes equations for flow between fixed parallel plates as discussed in another section. That is, |
|
|
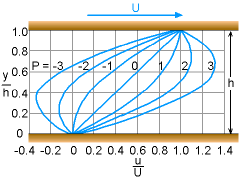
The velocity profile now becomes where P is the dimensionless pressure gradient, and is given by |
|
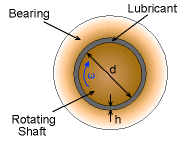 Journal Bearing |
The simple analysis mentioned thus far can be applied to journal bearings, which are widely used in mechanical systems. When the bearing is subjected to a small load, such that the rotating shaft and bearing remain concentric, the flow characteristic of the lubricant can be modeled as flow between parallel plates where the top plate moves at a constant velocity. The velocity of the lubricant in this situation is linear inside the gap, and it corresponds to the case where P = 0. | |
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.