| Ch 8. Strain Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Strain |
Mohr's Circle for Strain |
Strain Gages |
|||||
| Mohr's Circle for Strain | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Mohr's Circle - Strain |
Example |
|
|
Determine what diagram is the correct Mohr's circle for the given strain state. |
||
| Solution |
||
 Mohr's Circle - Strain |
The first step in constructing a Mohr's Circle is to locate its center along the normal strain axis (x-direction). center = (εx + εy)/2 = (100 + 400)/2 = 250μ Next, a point on the circle can be plotted, (εx, τxy/2) = (400μ, 100μ) These points are shown on the diagram on the left. Now the radius can be determined, R2 = 1002 + (400 - 250)2 The current stress state is represented by a line at an angle of θ = tan-1(100/15) = 33.69o Diagram 3 is the correct representative of Mohr's circle for the given strain state. |
|
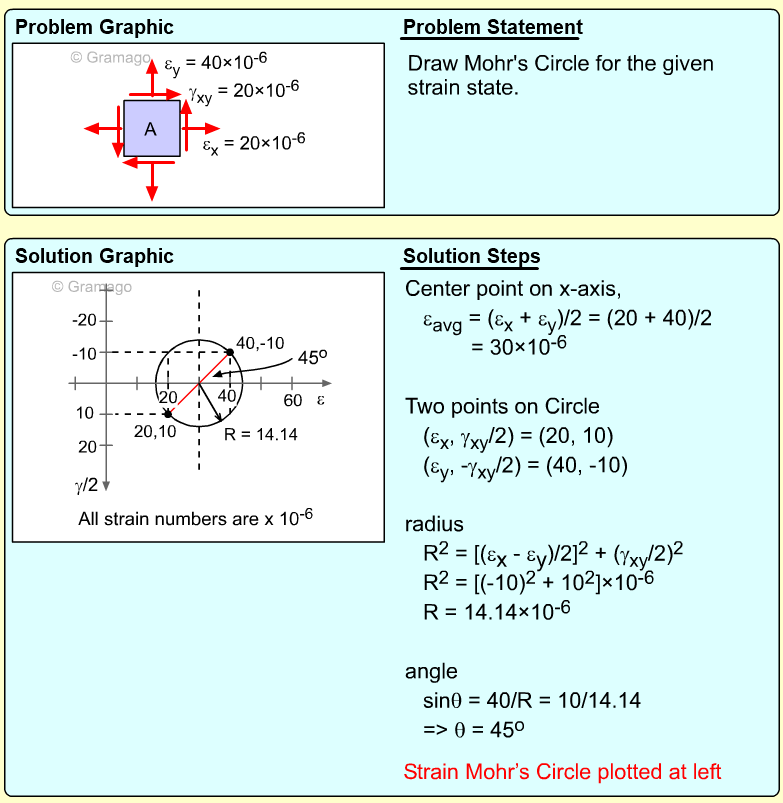
| Example Problem 1 |
||
|
||
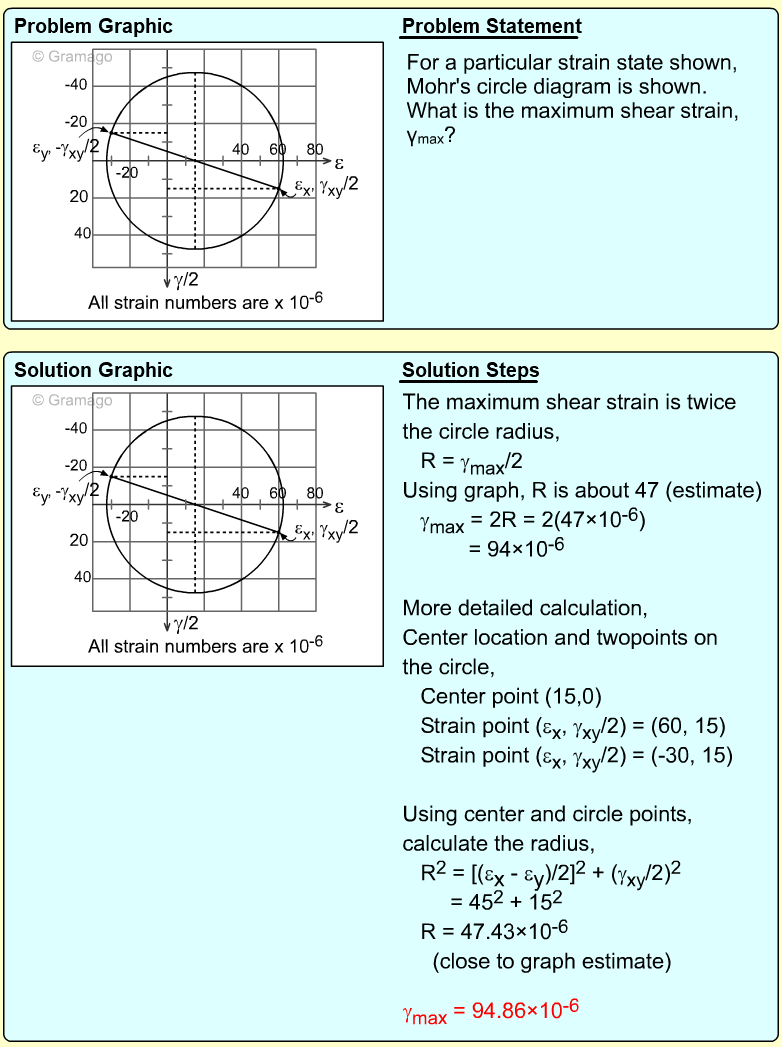
| Example Problem 2 |
||
|
||
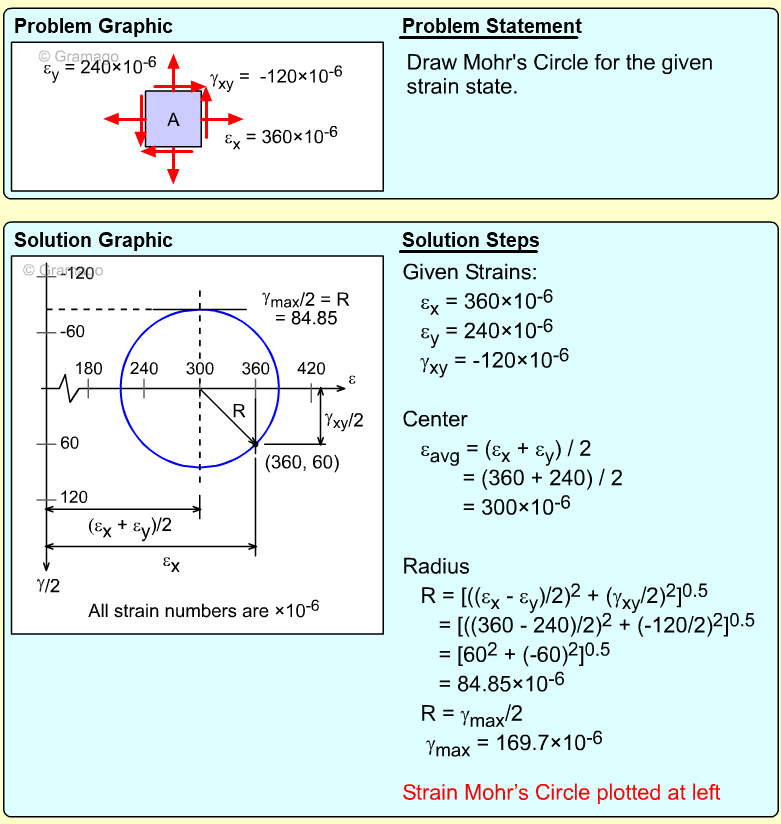
| Example Problem 3 |
||
|
||
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||