| Ch 8. Integration Techniques | Multimedia Engineering Math | ||||||
|
Integration by Parts |
Trig. Integrals Trig. Subst. |
Fractions & Substitutions |
Approximate Integration |
||||
| Trigonometric Integrals and Trigonometric Substitutions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
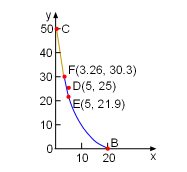
A man pulls a boat while he walks along a pier. A stone is located in the water where boat may travel when pulled. Determine if the boat will collide with the stone. |
||
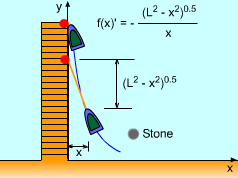 The Rope Tangent to the Curve |
First, consider the boat motion as then simply walks to the end of the pier. Since the rope is straight and tout as the man pulls the boat, the path followed by the boat will be a curve and the rope will be tangent to the curve. Therefore, the curve function is To find the above integral, use trigonometric substitution. Let x = Lsinθ and dx = Lcosθdθ |
|
The curve function becomes Now replace θ in the above equation by expression of x. x = Lsinθ After substituting, y becomes a function of x At point B shown on the left, x and y are known as x = L, y = 0. Substitute x and y into the above equation to find the constant C. After the man arrives at the end of the pier, he will pull the rope in with the rope. Then the path of the boat will be a straight line. To determine the line, the location of the boat just before the rope is pulled in needs to be determined. Assume F(x, y) is the boat location. The length CF equals the rope length L. |
||
|
Solve this equation with the path equation gives, x = 3.261 m Since 30.27 m> 25 m, the boat will pass by the stone (point D on the left diagram) before the man arrive the end of the pier. The stone is located at point D(5, 25). Substitute L = 20 and x = 5 into the path equation gives Since 21.90 m < 25 m, the boat will pass by the stone without collision. |
|