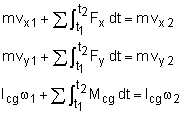| Ch 8. Rigid Body Momentum/Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse Momentum | Eccentric Impact | ||||||
| Principle of Impulse and Momentum | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
The Principle of Impulse and Momentum describes how an object's linear and angular momentum change with applied forces and moments. |
|||||
| Linear Impulse and Momentum |
|||||
|
|
Recall, from particle motion, the sum of external forces acting on a body equals the rate of change of linear momentum of the center of mass, Multiply both sides by dt and integrate from t = t1 to t = t2 to get This is known as the Principle of Linear Impulse and Momentum. It applies to both particle motion and rigid body motion. |
||||
| Angular Impulse and Momentum |
|||||
|
For a rigid body, the sum of external moments acting on the body about an axis through the center of gravity, cg, equals the rate of change of angular momentum about that axis, Multiply both sides by dt and integrate to get This is known as the Principle of Angular Impulse and Momentum about the cg. |
||||
 Linear and Angular Momentum Together |
If the motion of an object is in the x-y plane, then both the linear and angular equations can be used to write 3 scalar equations representing the components of linear and angular momentum, Many situations involve a fixed or pinned point, O. The angular momentum equation is then written as, It is the same as the previous form, but everything is based on the pinned point O. |
||||
| Conservation of Momentum |
|||||
 Constant Linear Momentum |
When the sum of external linear impulses acting on a system of rigid bodies or particles is zero, then the linear momentum is conserved, giving Σ(L)1 = Σ(L)2 Linear Momentum or This is the same equation that was developed for particle motion. This does not apply to an object that is pinned or fixed, since the reaction forces will produce an impulse. |
||||
 Constant Angular Momentum |
When the sum of external angular impulses acting on a system of rigid bodies or particles is zero, then the angular momentum is conserved, giving Σ(Ho)1 = Σ(Ho)2 Angular Momentum or This equation states that the total angular momentum of the system about a pinned or fixed axis O is conserved. |
||||