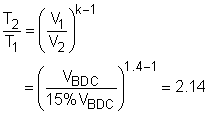In Max's senior capstone design, they need to determine the power generated and the thermal efficiency of the prototype engine supplied by the Handa Car Company.

Assumptions:

• Cold-air-standard assumption is valid for this analysis. The constant volume specific heat c_v = 0.718 kJ/kg.
• Model the cycle in the car engine as an ideal Otto cycle.
• Assume the total power generated by the four cylinders equals fou times of the power generated by one cylinder.

P-v and T-s Diagram of the
Otto Cycle

The P-v and T-s diagrams of an ideal Otto cycle are shown on the left. The working fluid contained in the cylinder of the car engine forms a closed system.

(1) Determine the power generated by this four-stroke-four-cylinder spark-ignition (SI) engine

In an Otto cycle, process 1-2 is an isentropic compression process. According to the data given, temperature and pressure at state 1 are

      T₁ = 15^oC
      P₁ = 100 kPa

Also, the T-s diagram shows the temperature of the air reaches its maximum value at state 3. That is,

      T₃ = 1800^oC

In the four processes of the Otto cycle, only processes 1-2 and 3-4 have work interaction. The energy balance in these two processes are,

       -w₁₂ = u₂ - u₁

      -w₃₄ = u₄ - u₃

The net work output is the sum of the work at process 1-2 and process 3-4.

      w_net = w₁₂ + w₃₄ = (u₁ - u₂) + (u₃ - u₄)
             = c_v(T₁ - T₂) + c_v(T₃ - T₄)

The cold-air-standard assumption states that the working fluid is air and modeled as an ideal gas, and all the processes are reversible. Hence, the relation between state 1 and 2 is

T₂ can be determined from the above relation.      

      T₂ = 2.14T₁ = 2.14(15 + 273) = 616.3 K = 343.3^oC

Since v₁ = v₄ and v₂ = v₃, and process 3-4 is an isentropic process,

T₃ is given as 1800^oC. Substitute T₁, T₂, and T₃ to the above equation gives T₄.

      T₄ = (288/616.3)(1800 + 273)
          = 968.7 K = 695.7^oC

Substitute all the data to the expression of the net work gives,

      w_net = c_v12(T₁ - T₂) + c_v34(T₃ - T₄)
             = 0.718(288 - 616.3) + 0.718(2073 - 968.7)
             = 557.2 kJ/kg

The mass of the air in the cylinder can be determined by the properties at state 1. First, the displacement volume is given as

      V_dis = 1 L = 0.001 m³

Using the relation between the volume at the bottom dead center (BDC), volume at the top dead center (TBC) and the displacement volume, the volume at the BDC, which equals V₁ can be determined as

      V_BDC = V_TBC + V_dis = 15%V_BDC + V_dis

      V₁= V_BDC = V_dis/85% = 0.00117 m³

At 15^oC and 100 kPa, the density of air is 1.2 kg/m³. The mass of the air in the cylinder is

      m = 1.2(0.00117) = 0.0014 kg

The total net work of one cylinder is

      W_net,one = 0.0014(557.2) = 0.78 kJ

The total power of four cylinders is

      W_net = 4(0.78) = 3.12 kJ

The piston of a four-stroke engine executes four strokes within the cylinder when the crankshaft completes two revolutions for each thermodynamic cycle. The crankshaft rotates at 2600 RPM. Thus, there is 1300 thermodynamic cycles per minute.

      W_{net, total} = (3.12)(1300)/60 = 67.6 kW

(2) Determine the thermal efficiency of the SI engine

The thermal efficiency for an Otto cycle is defined as

The compression rate is defined as the ratio of the volume of the air when the piston reaches its bottom dead center (BDC) to the volume of air when the piston reaches its top dead center (TDC).

      r =V_BDC/V_TDC = V_BDC/(15% V_BDC) = 6.7

Substitute r into the thermal efficiency expression gives,