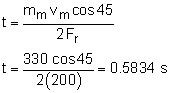| Ch 8. Rigid Body Momentum/Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse Momentum | Eccentric Impact | ||||||
| Principle of Impulse and Momentum | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
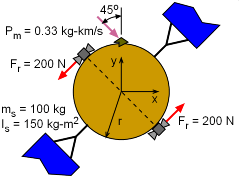 Problem Diagram with Coordinates |
To help simply the problem, consider a coordinate system that is attached to the satellite and moves with it. This will eliminates the satellite's orbital motion and it allows the problem to be solved like it is initially at rest. Also, the coordinate system should be rotated so that the impact point is on the y-axis. This will simplify the equations and calculations. |
|
| Meteoroid Impact - Linear Momentum |
||
|
|
Since the satellite is not initially spinning and is at rest, the total system linear momentum (both particle and satellite) is only in the meteoroid, or Lm = mmvm Assume that after the impact, the meteoroid becomes imbedded in the satellite. The linear momentum is Ls+m = (ms + mm) vs Since there are no external forces acting on the system, linear momentum must be conserved, or Lm = Ls+m Solving for the linear velocity of the satellite gives If the assumption is made that mm<< ms, then this reduces to = (0.33 kg-km/s)/(100 kg) = 3.3 m/s |
|
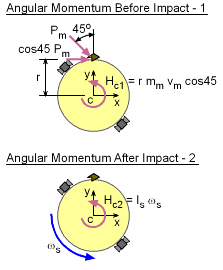
| Meteoroid Impact - Angular Momentum |
||
|
|
Just prior to impact, the angular momentum about the satellite center of the whole system (meteoroid and satellite) is Hc1 = - r mm vm cos45 This assumes that the particle momentum is zero or very small and has no effect on the overall angular momentum. Since after the impact the meteoroid is imbedded in the satellite, the angular momentum is Hc2 = Is ωs There are no other external moments in the system, so angular momentum must be conserved giving Hc2 = Hc1 Substituting for Hc1 and Hc2, gives the rotational or angular velocity of the satellite as |
|
| Thrusters - Linear Momentum |
||
|
Firing the thrusters applies a pure torque to the satellite; therefore, the linear momentum and hence the linear velocity of the satellite remains unchanged, |
||
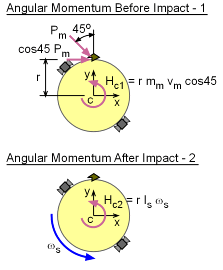
| Thrusters - Angular Momentum |
||
|
At this point, the satellite is spinning due to the particle impact and the thruster need to fire to stop this rotation. This requires the thruster to apply a moment impulse on the satellite. From the Principle of Impulse and Momentum, the integral of the applied moments about the center of rotation equals the change in angular momentum, The only applied moments to the system are the thrusters firing opposite the rotation: |
||
 Problem Graphic |
Integrating gives 2 r Fr t = -ωs2 Is Substituting for the angular velocity ωs gives, 2 r Fr t = -[-(r pm cos45) / Is] Is Notice, both Is and r terms cancel. Simplifying gives the required thruster firing-time to stop the rotation, It is interesting to note that the firing time does not depend on the satellite radius, r, or its moment of inertia, Is. |
|