| Ch 7. Inverse Functions | Multimedia Engineering Math | ||||||
|
Inverse Functions |
Exponential Functions |
Inverse Trig. Functions |
|||||
| Inverse Trigonometric Functions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||||||||||
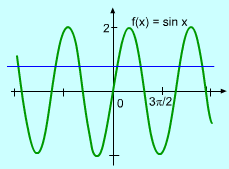 No Inverse Function for f(x) = sin x from -∞ to +∞ |
In this section, the method of finding the derivative of an inverse trigonometric function is introduced. It is known that trigonometric functions are not one-to-one function, and thus they do not have inverse function. However, trigonometric functions can be converted to one-to-one functions by restricting their domains. For example, function f(x) = sin x is not a one-to-one function from -∞ to +∞ and has no inverse function. This can be seen on the left figure. However, it is a one-to-one function from -π/2 to +π/2, and thus f(x) has inverse function in this range. |
|||||||||||||||||||||
| Arcsine Function |
||||||||||||||||||||||
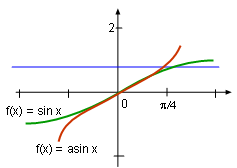 sin x and Its Inverse Function asin(x) from -π/2 to +π/2 |
The inverse function of f(x) = sin x is called the arcsine function. According to the definition of the inverse function, the following two equations are obtained and they are reciprocal inverse functions. sin-1x = y sin y = x for -π/2 ≤ y ≤ +π/2 The cancellation equation y = f(f -1(y)) and x = f -1(f(x)) for arcsine function becomes sin-1 (sin x) = x for -π/2 ≤ x ≤ +π/2 sin (sin-1 x) = x for -1≤ x ≤ +1 The derivative of an arcsine function can be calculated as where -1< x < +1 |
|||||||||||||||||||||
| Inverse Cosine Function |
||||||||||||||||||||||
The inverse cosine function is denoted by cos-1 or arccos. Its definition states: cos-1x = y cos y = x The cancellation equations for inverse cosine function are cos-1 (cos x) = x for 0 ≤ x ≤ π cos (cos-1 x) = x for -1 ≤ x ≤ +1 The derivative of the inverse cosine function is given by |
||||||||||||||||||||||
| Inverse Tangent Function |
||||||||||||||||||||||
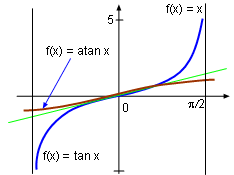 tan x and Its Inverse Function atan x in -π/2 to +π/2 |
The inverse tangent function is defined as the inverse function of tangent function and denoted as tan-1 or atan. Its domain is the interval (-π/2, +π/2). Its definition states: tan-1x = y tan y = x are reciprocal inverse functions where -π/2 ≤ y ≤ +π/2. The arctangent function is horizontal asymptotes because when x approaches +∞, 1/x is extremely close to +π/2 and when x approaches -∞, 1/x is extremely close to -π/2. This can be expressed with mathematics equations: and The derivative of the inverse arctangent function is given by |
|||||||||||||||||||||
| Other Inverse Trigonometric Function |
||||||||||||||||||||||
|
The definition of csc-1 is given by sec-1x = y for |x| ≥ 1 sec y = x for y ∈[0, π/2] ∪ [π/2, 0] The definition of csc-1 states csc-1x = y for |x| ≥ 1 csc y = x for y ∈(0, π/2] ∪ [π, 3π/2] The definition of cot-1states cot-1x =& y cot y = x for y ∈(0, π) |
|||||||||||||||||||||
| Derivative for Inverse Trigonometric Functions |
||||||||||||||||||||||
Inverse trigonometric functions also have integration and derivation. Some of the formulas are listed in the table. |
||||||||||||||||||||||