| Ch 7. Stress Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Stress |
Principal Stresses |
Mohr's Circle for Stress |
Failure |
Pressure Vessels |
|||
| Mohr's Circle for Stress | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Mohr's Circle |
Example |
|
|
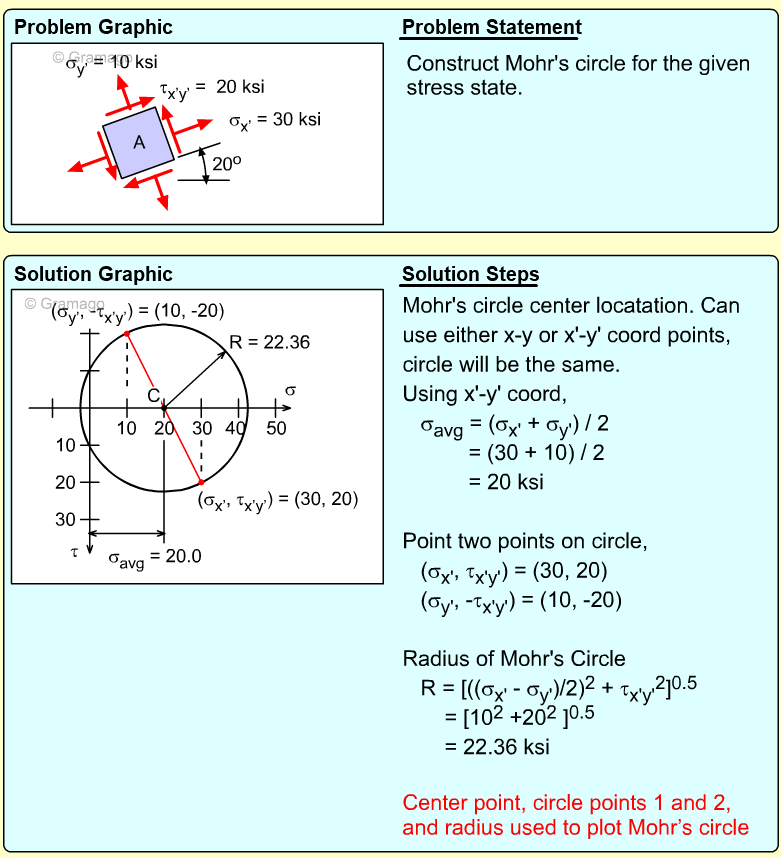
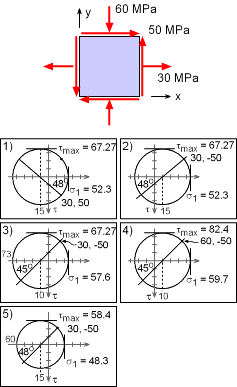
Which Mohr circle is correct for the given stress state
|
||
| Solution |
||
|
The given stress components for the stress element are, σx = 30 MPa |
||
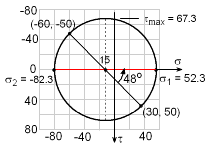 Rotated Stress Element |
Mohr's Circle center will be at the normal stress average, which is plotted on the diagram at the left. Next, a point on the circle is needed. Two different points can be used, Remember, the shear stress is plotted positive in the downward direction. From the plotted center and points on the circle, the radius (shear maximum) can be determined. R = τmax = [(30+15)2 + 502]1/2 = 67.3 MPa Principal stresses are σ1 = -15 + 67.3 = 52.3 MPa The principle direction is tan 2θ1 = 50/(15+30) The correct diagram is 1) |
|
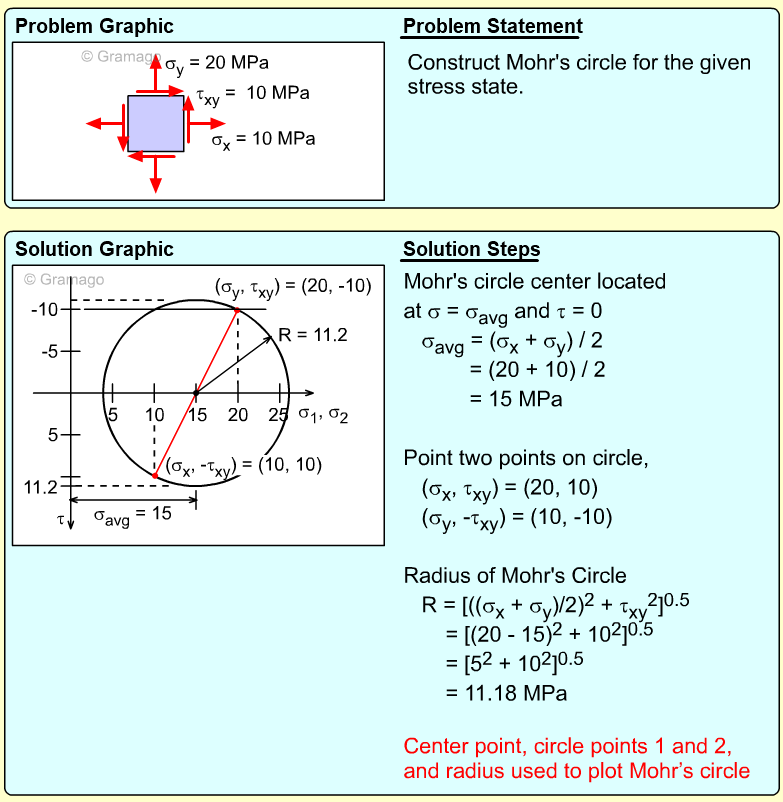
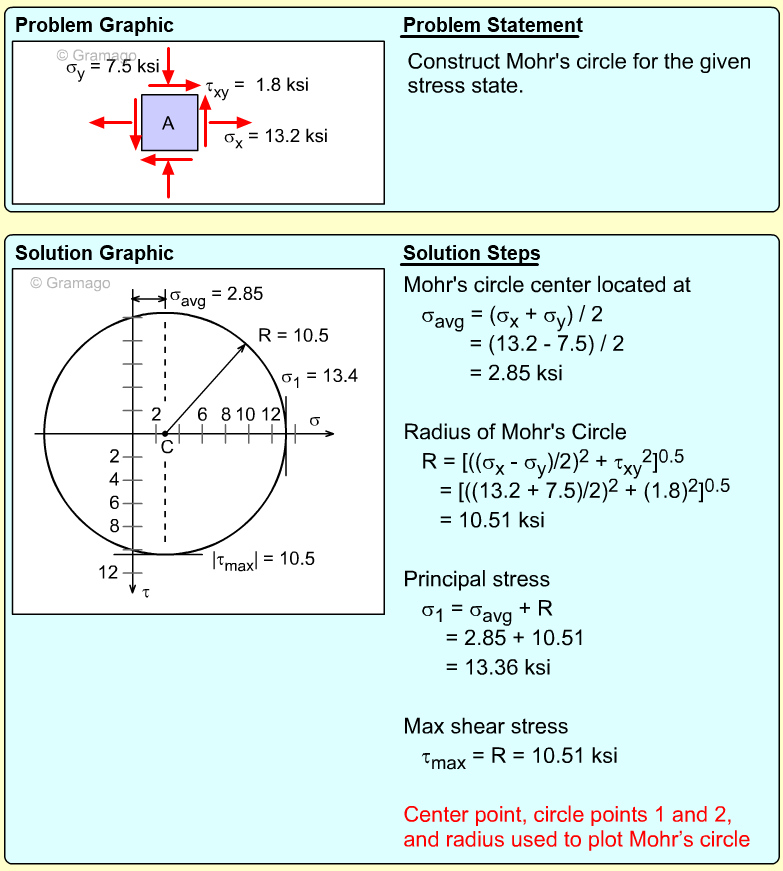
| Example Problem 1 |
||
|
||
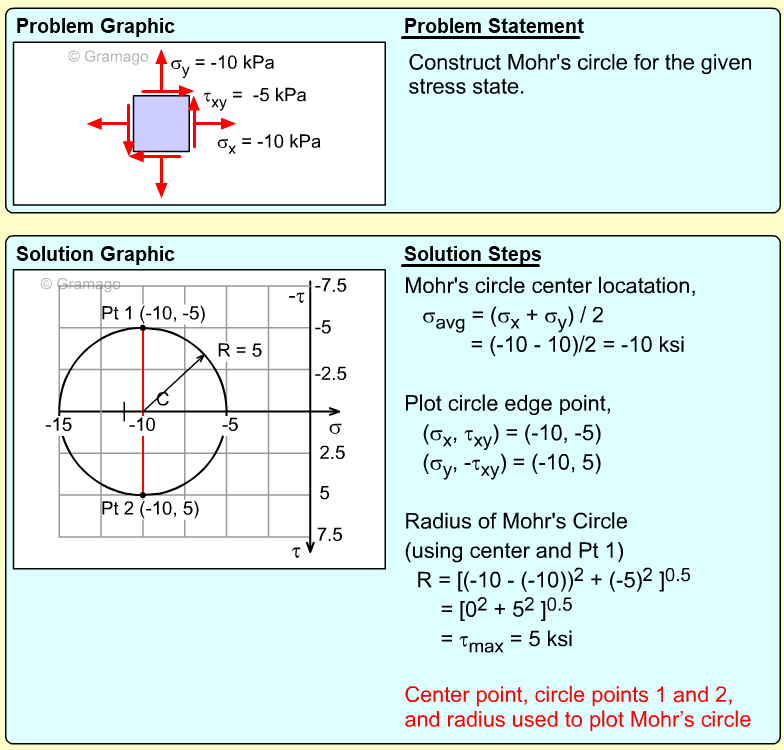
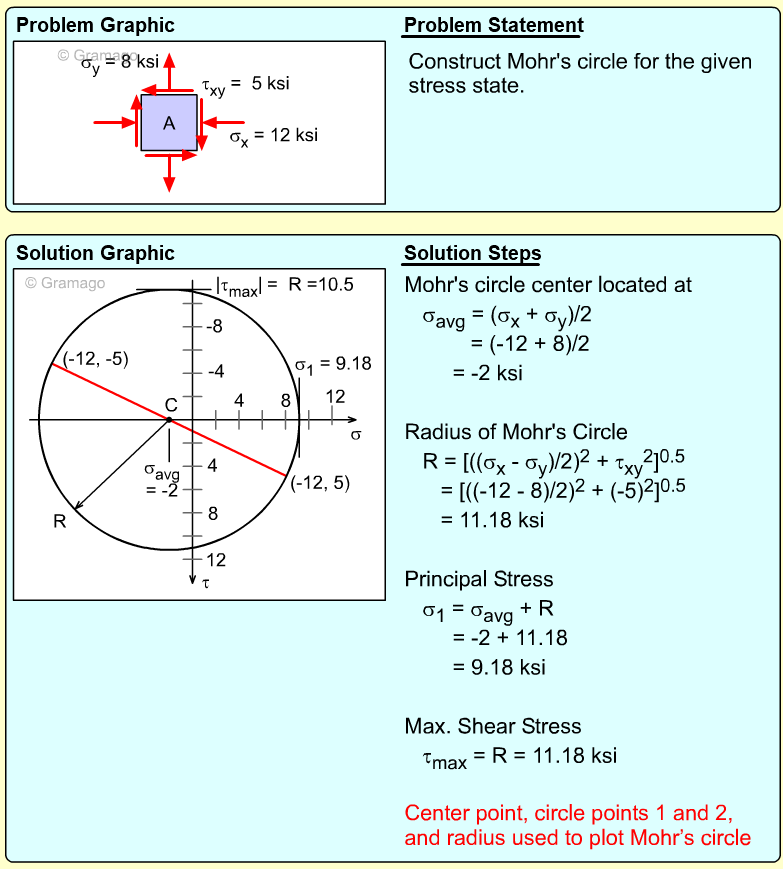
| Example Problem 2 |
||
|
||
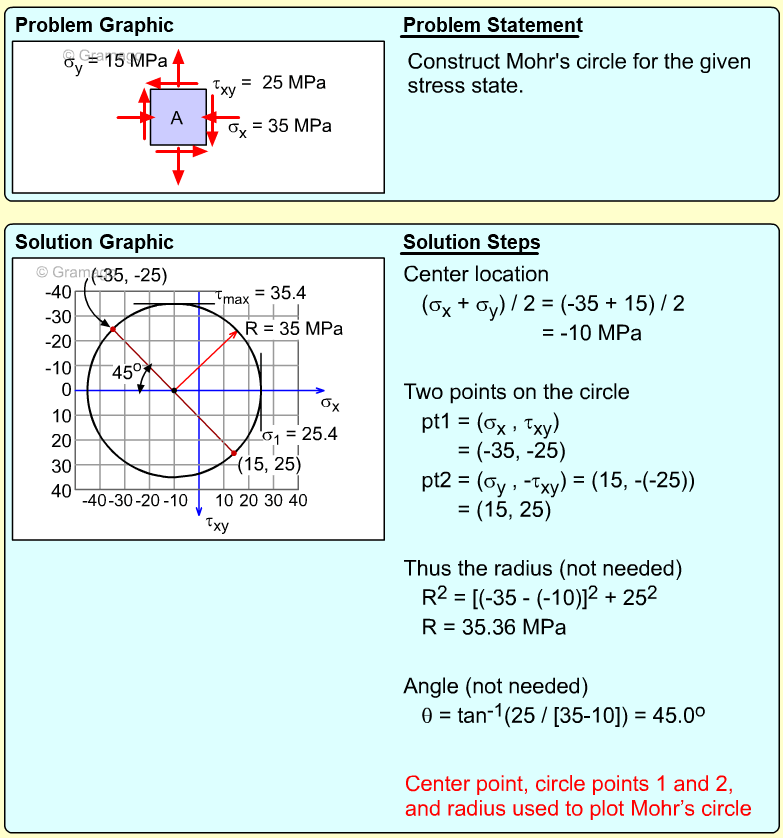
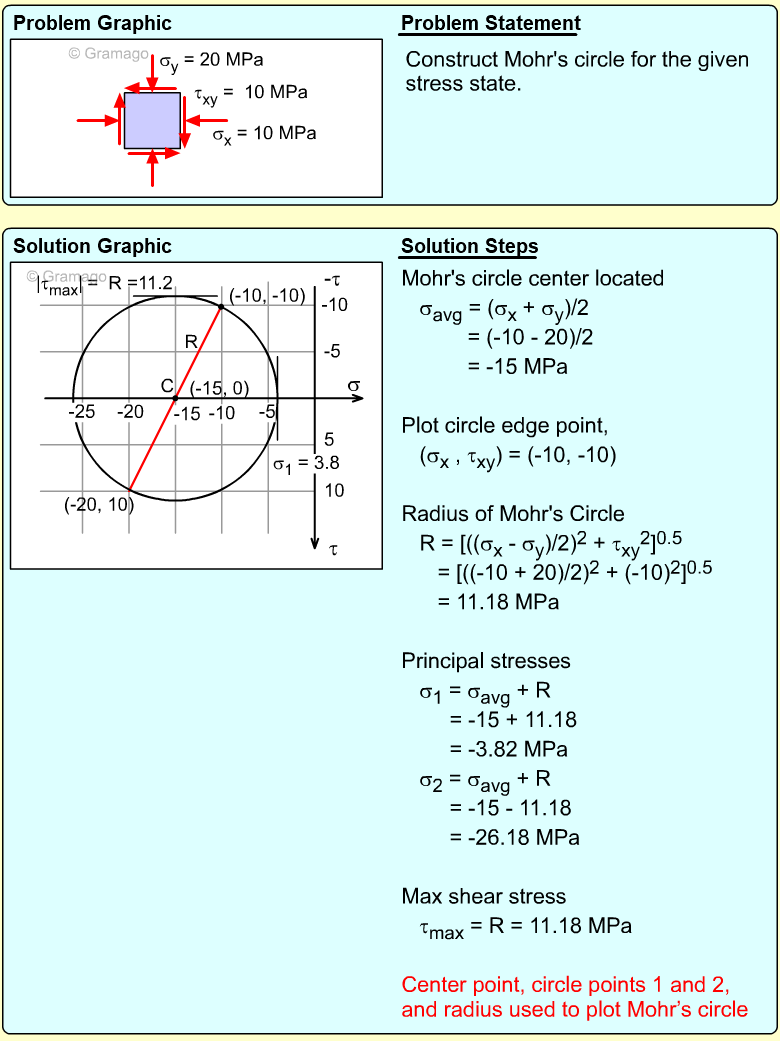
| Example Problem 3 |
||
|
||
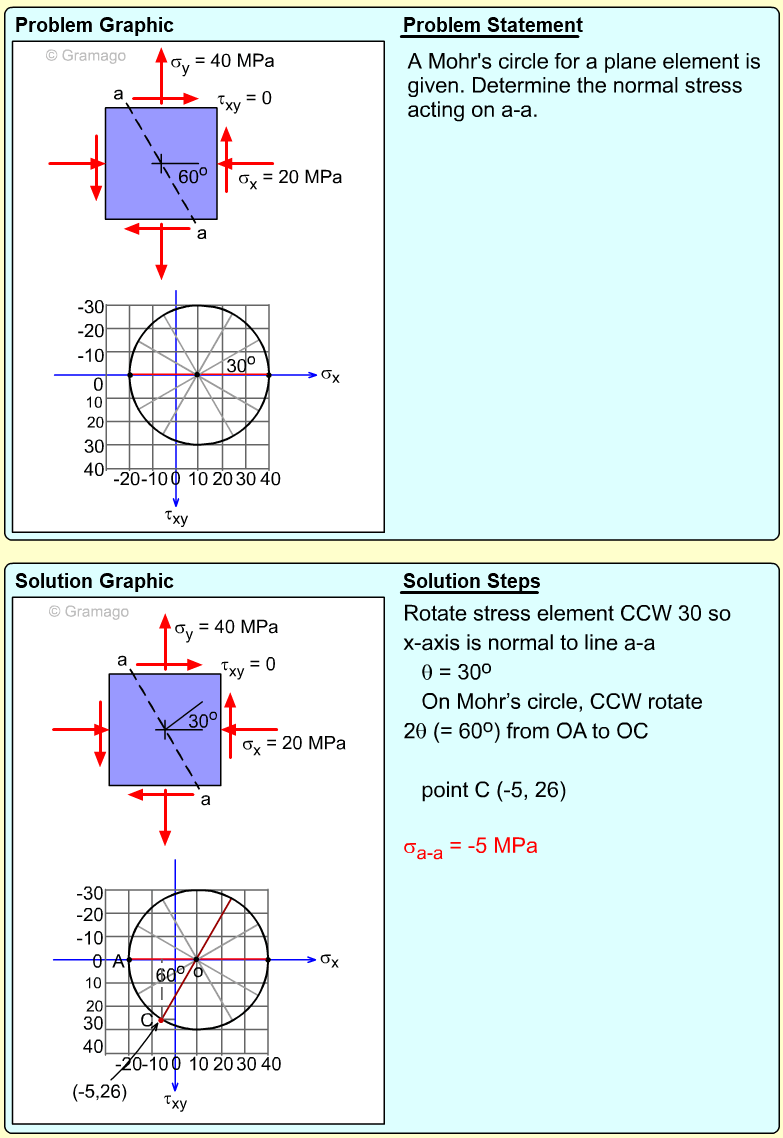
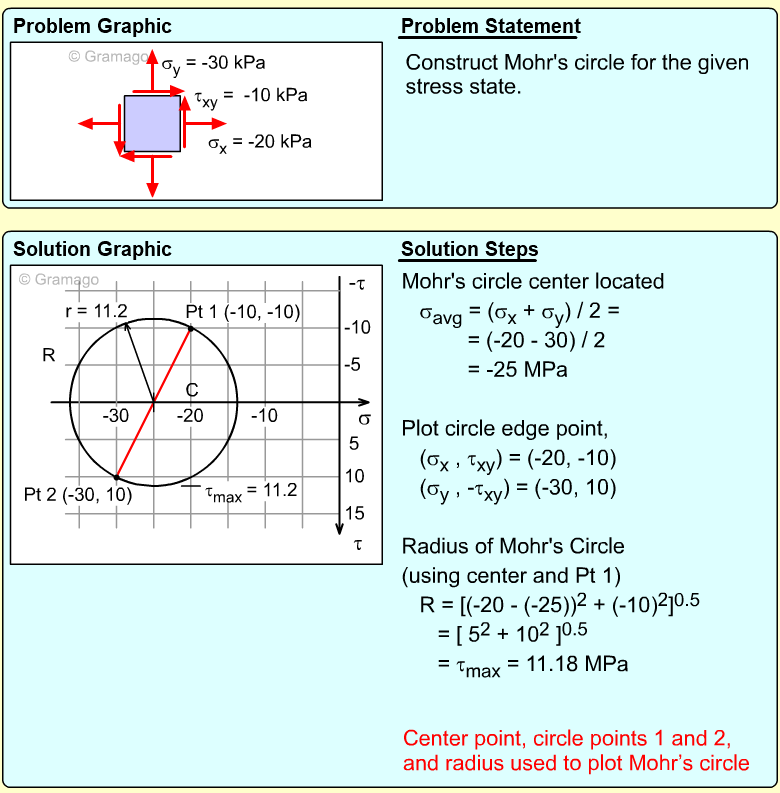
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||
| Example Problem 6 |
||
|
||
| Example Problem 7 |
||
|
||
| Example Problem 8 |
||
|
||
| Example Problem 9 |
||
|
||
| Example Problem 10 |
||
|
||
| Example Problem 11 |
||
|
||