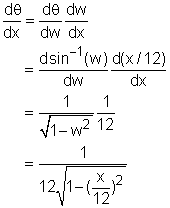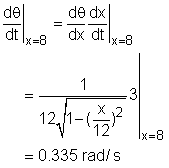| Ch 7. Inverse Functions | Multimedia Engineering Math | ||||||
|
Inverse Functions |
Exponential Functions |
Inverse Trig. Functions |
|||||
| Inverse Trigonometric Functions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
A 12 ft long ladder is sliding away from the base
of the wall at a speed of 3 ft/s. How fast
is the angle between the ladder and the wall changing when the bottom
of the ladder is 8 ft from the base of the wall? |
||
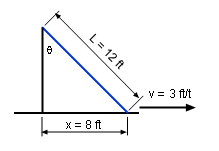 The State of the Ladder |
Let the angle made by the wall and the ladder be θ. Let the distance from the wall and the ladder be x. Let the length of the ladder and the sliding speed be L and v respectively. In trigonometry, the relationship between x, L and θ is: In order to find the changing rate of the angle, the angle θ needs to be determined first. The function of angle θ can be obtained by the inverse function of f(x) = sin θ. Therefore, θ = sin -1(x/12) The changing rate of the angle can be calculated by dθ/dt. Since the θ is a function of x, implicit differentiation method is used. dθ/dt = (dθ/dx)(dx/dt) In order to find dθ/dt, The derivative for inverse sine function and chain rule is used. Let w = x/12, the function θ can be expressed in terms of w as θ = sin -1(w) Therefore
It is given that the dx/dt = 3 ft/s. Thus the changing rate of the angle can be calculated. |
|