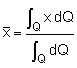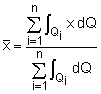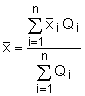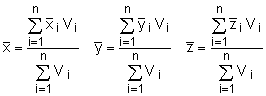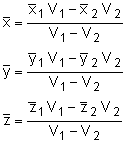| Ch 7. Centroid/Distributed Loads/Inertia | Multimedia Engineering Statics | ||||||
|
Centroid: Line Area Vol |
Centroid: Composite | Distributed Loads | Area Moment of Inertia | ||||
| Centroid: Composite Parts | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Equilibrium |
||
|
In the previous section, Centroid: Line, Area and Volume , it was shown that the centroid of an object involves evaluating integrals of the form where Q is a line, area, or volume, depending on the centroid that is required. The same equation can also be used for the other two directions by just substituting y or z for x. If there are several objects, then the centroid of the entire system is given by where n is the number of objects in the system. This equation can be simplify as where |
||
| Centroid of a System of Lines |
||
|
For a system of lines, the coordinates of the centroid are Here |
||
| Area Centroid of a System of Objects |
||
|
For a system of objects, the coordinates of the area centroid are Here |
||
| Volume Centroid of a System of Objects |
||
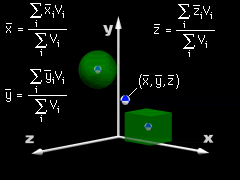 Centroid of Multiple Objects |
For a system of objects, the coordinates of the volume centroid are Here |
|
| Subtraction of Material (Holes) |
||
|
If an object or system of objects has a cutout or hole, then the centroid of the system can be found by considering the cutout or hole as a negative area, volume, or line length. For example, if a system consists of a cube with a centroid at x1, y1, z1 and a volume of V1; and a hole within the cube that has a centroid at x2, y2, z2 and a volume of V2; then the coordinates of the centroid for the system are |
||