| Ch 7. Inverse Functions | Multimedia Engineering Math | ||||||
|
Inverse Functions |
Exponential Functions |
Inverse Trig. Functions |
|||||
| Exponential Growth and Decay | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
This section discusses the concept of exponential functions and their derivatives. |
||
| Exponential function |
||
An exponential function is in the form of f(x) = ax, where a is a positive constant. This function is defined in five segments:
|
||
Exponential function has some properties that are useful for calculating its value. They are given below.
In some intervals, an exponential function is continuous and differentiable. The properties of the exponential function that relates its derivation is given in the next section. |
||
| Derivatives of Exponential Functions |
||
If the exponential function, f(x) = ax, is differentiable at 0, then it is differentiable everywhere in its interval and f(x) = f '(0)ax This equation means the rate of change of any exponential function is proportional to the function itself and this equation is exponential growth/decay equation. The increasing of the population is an example of exponential growth and the cooling of bodies is an exponential decay. In the equation f(x) = f '(0)ax, there must be an "a" such that f '(a) = 1. Traditionally, this "a" is denoted by the letter e, such that The derivative of the exponential function f(x) = ex is its function value which can be expressed as dex/dx = ex The exponential function f(x) = ex is an increasing continuous function in its domain. Its value is positive and |
||
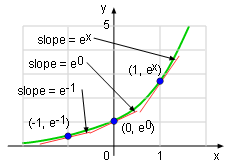 The Exponential Function f(x) = ex |
When plotted, the slope of a tangent line to the curve y = ex is equal to the y coordination of that point as shown on the left. The Chain Rule can be apply to exponential function to facilitate the calculation of its derivative. deu/dx = eudu/dx The exponential function can also be integrated and its value is in which c is a constant. |
|