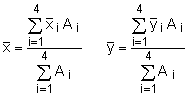| Ch 7. Centroid/Distributed Loads/Inertia | Multimedia Engineering Statics | ||||||
|
Centroid: Line Area Vol |
Centroid: Composite | Distributed Loads | Area Moment of Inertia | ||||
| Centroid: Composite Parts | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
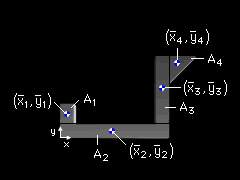
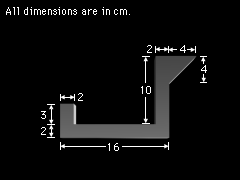
The beam cross section can be broken into 4 composite parts consisting of 3 rectangles and a triangle as shown. Orient an axis system as shown, so that the cross section lies entirely in the x-y plane. Since the thickness is constant for all the parts, the centroid can be found using the area equations,
|
|
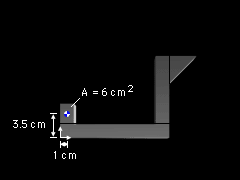
| Composite Part 1 |
||
|
|
Part 1 is a rectangle with an area of A1 = (2)(3) = 6 cm2 The centroid of a rectangle lies at half its width and half its height, so for part 1
|
|
| Composite Part 2 |
||
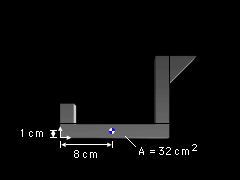 Part 2 |
Part 2 is a rectangle with an area of A2 = (16)(2) = 32 cm2 Its centroid is located at
|
|
| Composite Part 3 |
||
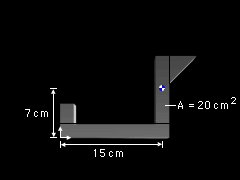 Part 3 |
Part 3 is a rectangle with an area of A3 = (2)(10) = 20 cm2 Its centroid is located at
|
|
| Composite Part 4 |
||
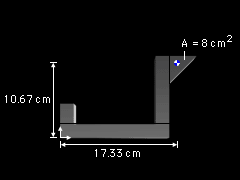 Part 4 |
Part 4 is a triangle with an area of A4 = (0.5)(4)(4) = 8 cm2 The centroid of a right triangle is located two-thirds of the distance from the vertex to the other end; therefore, for part 4
|
|
| Centroid of Total System |
||
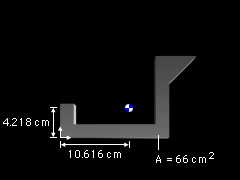 Total System |
With these results, find the total area of the system is Substituting the areas and centroid locations for each of the individual parts into the first two equations gives
|
|