| Ch 7. Inverse Functions | Multimedia Engineering Math | ||||||
|
Inverse Functions |
Exponential Functions |
Inverse Trig. Functions |
|||||
| Inverse Functions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
This section introduces the concept of an inverse function and its properties. |
||
| One-to-One Function |
||
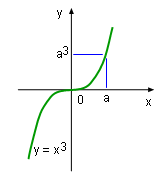 one-to-one Function f(x) = x3 |
Since only a one-to-one function has an inverse function, this section will first introduce the concept of a one-to-one function. If a function has a unique function value for each element in the domain, then this function is a one-to-one function. This concept can be expressed with mathematics as f(x1) ≠ f(x2) whenever x1≠ x2 For example, the function f(x) = x3 is a one-to-one function because no two x values can have the same f(x) value as seen on the diagram. |
|
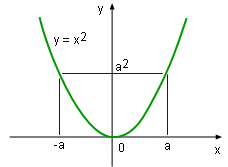 Not a one-to-one Function f(x) = x2 |
On the other hand, function f(x) = x2 is not a one-to-one function because when x equals either +a or -a, the function value is a2 see diagram. The method used to determine whether a function is a one-to-one function or not is called the Horizontal line test. | |
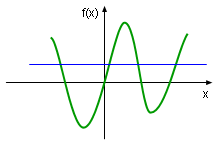 Horizontal Line Test Intersects Graph More Than Once |
The horizontal line test gives a geometric method to determine whether a function is one-to-one function. It states: a function is a one-to-one function if and only if no horizontal line intersects its graph more than once. For example, the function on the left is not a one-to-one function. Actually, all decreasing and increasing functions are one-to-one function and only one-to-one functions can have inverse function. | |
| Inverse Function |
||
The definition of inverse function states: Suppose the domain and the range of a one-to-one function f is R1 and R2 respectively. Then its inverse function f -1 has R2 and R1 as its domain and range, and f -1 is defined by f -1(y) = x <=> f(x) = y for any y in R2. Notice that in this definition, f -1 is not an exponent which means f -1(x) ≠ 1/f(x) |
||
|
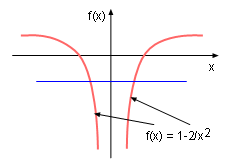
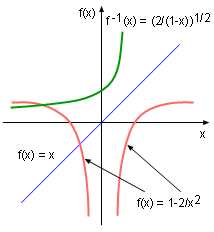
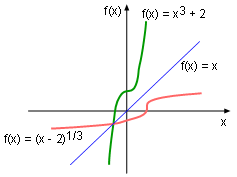
In order to find the inverse function, the equation for x needs to be solved in terms of y, and then switch x with y. To better under this method, the process of finding the inverse function of f(x) = 1 - 2/x2 when x > 0 is presented. First, rearranging the equation in terms of x gives: 2/x2 = 1 - y x = (2/(1 - y))1/2 Then switching x with y gives: y = (2/(1 - x))1/2 Therefore the inverse function is f -1(x) = (2/(1 - x))1/2. Notice that the domain of this example is x > 0, this is because the function is a one-to-one function in this range. However, in the domain of (-∞, ∞), the function is not a one-to-one function as shown on the left, and thus there is no inverse function in this domain. The inverse function can also be determined using a geometric method by reflecting the graph of the function with respect to the line y = x. The graphic on the left shows function f(x) = 1 - 2/x2 and its inverse function f -1(x) = (2/(1 - x))1/2 are symmetric with respect to y = x in the range between 0 and +∞. Various theorem related to inverse functions that are given in the following paraghaphs, will help to determine the continuity and differentiability of a function. |
|
| Theorem About Continuous |
||
 Continuous Function f(x) and f '(x) |
If a one-to-one function is continuous in its domain, then its inverse function is also continuous. Some of the continuous function are differentiable, so do the inverse function. The theorem related to the derivative of inverse functions is introduced below. |
|
| Theorem About Differentiable |
||
 Differentiable Inverse Function Example |
If a one-to-one function is differentiable and the derivative of its inverse function is not zero at a point, than the inverse function is differentiable at this point and g '(a) = 1/f '(g(a)) in which g is the inverse function of function f. In order to master this concept, find g '(8) in which g '(x) is the inverse function of f(x) = x3. It can be calculated that f(2) = 8 Therefore, switching x and y gives the value of the inverse function which is g(8) = 2 Since function f(x) is a one-to-one increasing continuous function, its derivative is f '(x) = 3x2 Using the theorem about differentiable gives g '(8) = 1/f '(g(8)) = 1/f '(2) = 1/(3(2)2) = 1/12 |
|