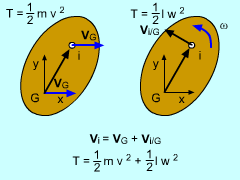Energy Balance

Force
Moment
Gravity
Friction
Spring

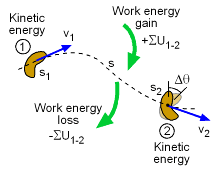
The Principle of Work and Energy equates the total work performed on a body to the change in kinetic energy,

     Σ Work = Δ Kinetic Energy

Another way to express this concept is

where
     T₁ = kinetic energy (translational and rotational)
                at position 1
     T₂ = kinetic energy (translational and rotational)
                at position 2
     ΣU_1-2 = total change in energy (i.e. work)
                   between positions 1 and 2

Work on a rigid body is the same as work on a particle, with the addition of rotational energy. Recall from Particle Energy Methods section, there are various ways to model energy for a particle. These are listed in the table at the left.

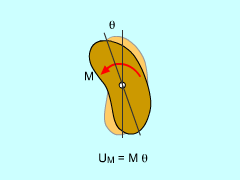
The work of two parallel, non-collinear forces in opposite directions with equal magnitudes forms a couple and moment. This moment generate energy similar to a linear force through a distance. However, the distance is now the angle of rotation.

Rotational and Translational
Kinetic Energy

For a particle that has no rotation, the kinetic energy is simply,

     T = 1/2 m v²

This equation can be applied to every particle that makes up a rigid body,

However, if the particle is a rigid body with dimensions, then the velocity needs to be written as

where G is the center of gravity. The second terms models the rotation of the object. Substituting v_i into the kinetic equation and noting that a magnitude of v_i/G = r_i/G ω gives

If the rigid body has a fixed point, then the equation becomes

     T = 1/2 I_o ω²

where I_o is moment of inertia about the fixed point.