| Ch 7. Centroid/Distributed Loads/Inertia | Multimedia Engineering Statics | ||||||
|
Centroid: Line Area Vol |
Centroid: Composite | Distributed Loads | Area Moment of Inertia | ||||
| Centroid: Line, Area and Volume | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Introduction |
||
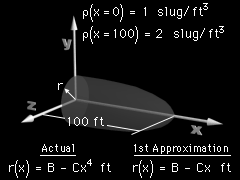 Geometry Diagram |
In order to determine a submarine's buoyancy characteristics, designers must accurately determine the centroid, center of mass, and center of gravity for various parts of the sub. What is known:
|
|
| Question |
||
|
|
As a first approximation, assume the nose code is a simple cone shape (D = 1 in the above equation). Where is the centroid, center of mass, and center of gravity? |
|
| Approach |
||
|
||
