| Ch 6. Integrals | Multimedia Engineering Math | ||||||
|
Indefinite Integral |
Area |
Definite Integral |
Fundamental Theorem |
Substitution Rule |
|||
| Substitution Rule | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
In indefinite integral section, various formulas have been introduced to calculate the integral of a function. However, it is not possible to have a formula for every possible situation. Thus, basic formulas like need to be generalized so they can be used in a variety of cases. This rule is called the substitution rule. |
||
| The Substitution Rule for Indefinite Integrals |
||
The substitution rule states: If u = g(x) is a differentiable function in an interval R and f is continuous on R, then |
||
|
This rule can be better understand by calculating
Let u = 5x2 + 7. The derivative of u with respect to x is du/dx = 10x Rearrange the above equation gives du = 10xdx Thus 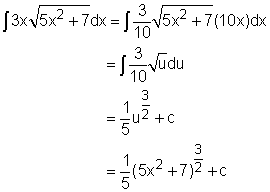 |
|
In order to double check the answer, the derivative of
function The result confirms the correction of |
||
| The Substitution Rule for Definite Integrals |
||
Substitution rule can also be used for definite integrals. The substitution rule for definite integrals states: If g'(x) is continuous on interval R and f(x) is continuous on the range of g(x), then |
||
This rule can be better understand by calculating
Let u = 5x2 + 7. The derivative of u with respect to x is du/dx = 10x Rearrange the above equation gives du = 10xdx The new limits of integration can be calculated. When x = 0, u = 7 and when x = 1, u = 12. Therefore, It is obviously that the substitution rule provides an easy way to calculate the integral of a function. |
||
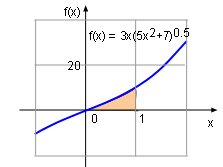
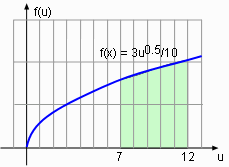
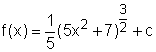 can
be taken.
can
be taken.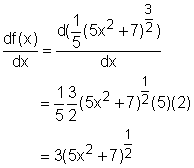
 .
.