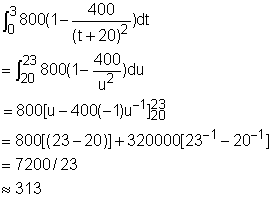| Ch 6. Integrals | Multimedia Engineering Math | ||||||
|
Indefinite Integral |
Area |
Definite Integral |
Fundamental Theorem |
Substitution Rule |
|||
| Substitution Rule | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
|
Substitution Function for the |
Lansing automobile company is manufacturing a new model of car with a produce rate of How many cars can be produced in the first season? The output of the car is the integral of the production rate with respect to time in the range between 0 and 3 months. Let u = t + 20. The derivative of u with respect to time t is du/dt = 1 Rearrange the above equation gives du = dt The new limits of integration can be calculated. When t = 0, u = 20 and when t = 3, u = 23. The substitution rule gives that Thererfore, |
|