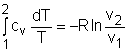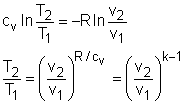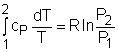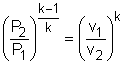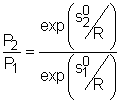| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Isentropic Process | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Isentropic Processes
|
||
|
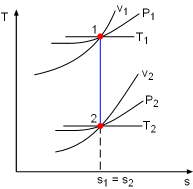
The term "isentropic" means constant entropy. A process during which the entropy remains constant is called an isentropic process, which is characterized by ΔS = 0 or s1 = s2 for a process 1-2 If a process is both reversible and adiabatic, then it is an isentropic process. An isentropic process is an idealization of an actual process, and serves as a limiting case for an actual process. |
|
| Isentropic Processes for Ideal Gases
|
|
The relations of entropy change for ideal gases are By setting Δs to 0 in the above
equations, the relations for an ideal gas which undergoes an isentropic
process can be obtained. Setting equation (1) to zero gives, |
|
|
If the constant-specific-heats assumption is valid, the above equation can be integrated and rearranged to give where The second relation can be obtained by setting equation (2) to zero. Also, if the constant-specific-heats assumption is valid, the above equation becomes The third relation can be obtained by combining the first and the second relations. That is, The three relations of an isentropic process for ideal gases with constant specific heats in compact form are Tvk-1 = constant |
|
|
|
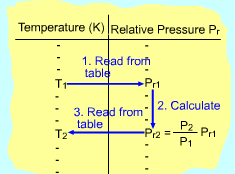
If the constant-specific-heats assumption is not valid, the entropy change of ideal gases during a process 1-2 is Setting the above equation to zero and rearranging, one obtains If exp(s0/R) is defined as the relative pressure Pr, then the above equation becomes (P2/P1)s = constant = Pr2/Pr1 Values of relative pressure are tabulated against temperature in
tables. |
|
|
|
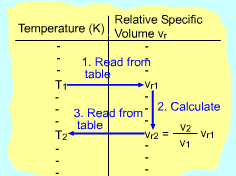
In an automotive engine, the ratio v2/ v1 is used instead of the ratio P2/ P1. The ideal-gas relation gives v2/ v1 = T2P1/T1P2 Replacing P2/P1 by Pr2/Pr1 in the above equation gives T/Pr is defined as relative specific volume vr and its value is also tabulated with temperature. Thus, (v2/v1)s = constant = vr2/ vr1 |
|
| Isentropic Processes for an Incompressible Fluid or
Solid
|
||
|
|
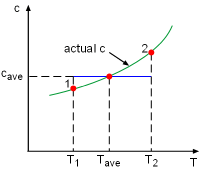
The entropy change of incompressible fluids or solids during a process 1-2 with constant specific heats is Δs = caveln(T2/T1) Setting Δs to zero gives T2 = T1 That is, an isentropic process of an incompressible substance is also isothermal. |
|
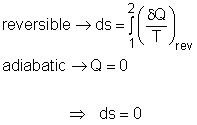

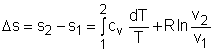 (1)
(1)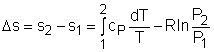 (2)
(2)