| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| General Plane Motion | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
|
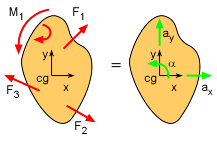
If a rigid body moves with both translational and rotational motion, it is said to be in general plane motion. To analyze general plane motion, equations describing the translation of the center of gravity and the equations describing the rotation need to be used. The detailed derivation is omitted, but as expected, the 2D rigid body equations include three equations,
All three equations must be applied to the center of gravity point, cg, but there is no assumption that the object is pinned. If there is a fixed axis (any location), as discussed in the previous section, then these equation simplify to a single equation since there is no translation at the fixed point, o, ΣMo = Io
α (point o is fixed axis) If the translational motion and the rotational motion are not independent, there may be more unknown quantities than equations of motion. In these cases, additional equations can be derived by relating the translational acceleration of the center of mass to the rotational acceleration. |
||||
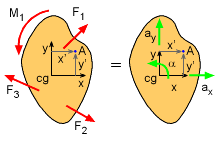 General Motion Force and Acceleration Diagrams around an Arbitrary Point |
Sometimes, it useful to take sum forces and moments about a point that is neither fixed or the center of gravity. Then the three basic equations become, ΣFx = macg-x ΣFy = macg-y ΣMA = Icg α - x' macg-y + y' macg-x Note that the moment equation as two additional terms on the right side to compensate for the fact that the moments are being applied to the point other than a fixed point or the center of gravity. |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.