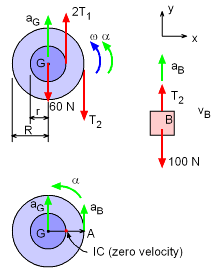
A spool, G, is hung from a ceiling and a block, B, is attached to its outer surface with a cable as shown. The block weighs 100 N and the spool weighs 60 N. The spool's radius of gyration is 3 cm with respect to its mass center, G. It has outer radius, R, of 4 cm and inner radius, r, of 2 cm. If the system is released from rest in the position shown, what is the acceleration of the mass center G?

Angular Velocity and Acceleration

The equations of motion for the block,
     ΣF_y = m a_By
     T₂ - 100 = (100/9.81) a_By
     T₂ = 100 + 10.19 a_By

The vertical equation of motion for the spool,
     ΣF_y = m a_Gy
     2T₁ - T₂ = 60 + (60/9.81) a_Gy 
     2T₁ - T₂ = 60 + 6.116 a_Gy 

The angular equation of motion about point G,
     ΣM_Gz = I_Gzα
     2T₁(0.02) - T₂(0.04) = mk² α
     0.04T₁ - 0.04T₂ = (60/9.81)(0.03)² α
     T₁ - T₂ = 0.1376 α

These three equations have five unknowns, so additional relationships need to be identified. One idea is to use the IC point to relate α and the two linear accelerations, a_Gy and a_B. At the instant given, the spool is pivoting around the point where the ceiling cable is attached to the spool, and thus has zero velocity. Thus,
      a_Gy = r_Gα = -0.02 α
      a_By = r_Bα = 0.02 α

Putting these into the above three equations,
     T₂ = 100 + 0.2038 α
     2T₁ - T₂ = 60 - 0.1223 α 
     T₁ - T₂ = 0.1376α

Combining into two equations,
     2T₁ = 100 + 0.2038 α + 60 - 0.1223 α 
     T₁ = 100 + 0.2038 α + 0.1376α

Eliminate T₁, gives,
     α = -66.52 rad/s²

Thus, the spool center, G, is accelerating upward,

a_Gy = 1.330 m/s²