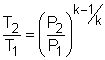| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Isentropic Process | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
A leak develops in a well-insulated bottle initially containing compressed carbon dioxide. The mass of carbon dioxide left in the bottle needs to be determined. Assumptions:
|
||
|
Molar Mass, Gas Constant for Various Common Gases
Specific Heats of Some
|
Take the bottle as the system. Denote the state before leak as state 1 and the state after leak as state 2. From the assumptions made, carbon dioxide is modeled as an idea gas. With the ideal-gas equation of state, the mass remains in the bottle after leak is m2 = P2V2/RT2 where P2 and V2 are known. If the temperature T2 is determined, the mass remaining m2 can be obtained. The gas constant R of carbon dioxide is 188.9 J(kg-K). The leaking process is adiabatic and reversible, hence it is an isentropic process. The second relation of isentropic process for ideal gases is: Assume the final temperature is 350 K and use the average value of the initial temperature and the final temperature to determine the value of k. Tav = (500 + 350 )/2 = 425 K From the table, k equals to 1.246 at 425 K. With all the data known, T2 can be obtained by substituting the values of T1, P1, and P2 into the above equation. T2 = 500(1/5)0.246/1.246 = 363.9 K The calculated final temperature is close to 350 K (the assumed temperature), hence no iteration is needed. Inserting T2, P2, and V2 into the expression for m2 gives, m2 = (101,325)(200/1,000)/((188.9)(363.9)) |
|