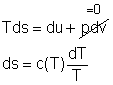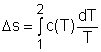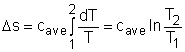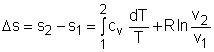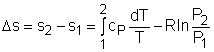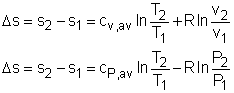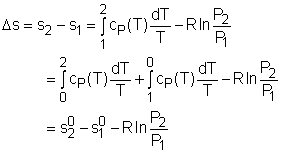| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Entropy Change | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||
| Entropy Change of Pure Substances
|
|||||
 The Entropy of a Pure Substance Determined by Tables |
The entropy of a pure substance is determined from tables in the same manner as other properties such as v, u, and h. The value of entropy at a specified state is determined just like any other property.
If the compressed liquid data are not available, the entropy of the compressed liquid can be approximated by the saturated liquid at the same temperature. scompressed@T,P = sf@T |
||||
|
|||||
| Entropy
Change of Solids and Liquids
|
For an incompressible substances, the specific volume does not change during a process. That is, dv = 0 The internal energy of an incompressible substance is du = c(T) dT Most solids and liquids can be approximated as incompressible substances. The entropy change of solids and liquids can be obtained by applying the above two equations to the first Tds equation. The entropy change during a process 1-2 is |
||||
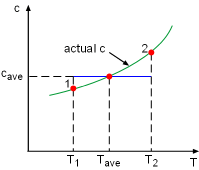 Constant Specific Heat Used in Small Temperature Interval |
If the temperature variation (T2 - T1) is small over the entire process, an average specific heat (cave) is used and treated as a constant (constant-specific-heats assumption). Then the entropy change can be evaluated by |
||||
| Entropy Change of Ideal Gases
| |||||
The property relations for ideal gases are: pv = RT The first relation of entropy change for ideal gases is obtained by replacing P by RT/v and du by cvdT in the first Tds equation: Tds = du + Pdv ds = cvdT/T + Rdv/v Integrating ds from state 1 to state 2 gives the first relation of entropy change for ideal gases. The second relation of entropy change for ideal gases is obtained by replacing v by RT/P and dh by cPdT in the second Tds equation: Tds = dh - vdP ds = cPdT/T - RdP/P Integrating ds from state 1 to state 2 gives the second relation of entropy change for ideal gases. A common approximation is made by assuming that the specific heats of ideal gases are constants if the temperature variation is small (constant-specific-heats assumption). Replacing cv and cP with constants cv,av and cP,av in the first and second relations of entropy change and integrating from state 1 to state 2 gives, |
|||||
Ideal-gas Properties of Air Table
|
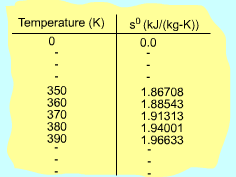
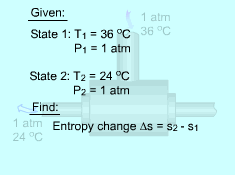
If the temperature variation is large, the variation of specific heats with temperature should be considered and relations between cv(T), cP(T) and temperature are needed to integrate the first and second relations. For convenience, a function s0, standard-state entropy, is defined as s0 is a function of temperature only and is tabulated with temperature. Absolute zero is used as the reference temperature. Replacing T as T1 and T2 in the above definition gives Then the entropy change of ideal gases during a process 1-2 is |
||||