| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Rotation about a Fixed plane | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
|
In the previous section, the basic equation for rigid body translational motion where given. However, in many situations, there is rotational motion about a fixed point in addition to the translational motion. This section presents those additional equation. However, the complete 2D general plane motion equations are given in the next section. |
|||||||
| Rotation About a Fixed Axis |
||||||||
|
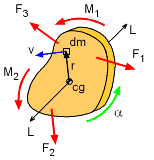
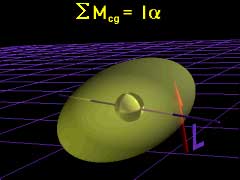
Rotation about a fixed axis is a simplification of the general plane motion. However, since a large number of real application involve fixed axis rotation, those equations are presented. The translation equations are still valid since the rotation axis may not be at the center of gravity. Recall, the total force acting on a rigid body equals the rate of change in linear momentum of the body's center of gravity. This gives, F = dL/dt = d(mvcg)/dt Similarly, angular acceleration can be related to the change of angular momentum, H. The total moment acting about an axis L passing through the center of gravity of a rigid body equals the rate of change in angular momentum about the axis L, or ΣMcg = d(Hcg)/dt Recall, for particles rotating about an axis, the angular moment is H = Σ(ri × mivi) If the rigid body is assumed to be constructed from an infinite number of particles, they can all be summed together, giving, ΣMcg = d[ Σ(rimi (riω)] / dt Notice, the cross product is removed since all particles are moving perpendicular to the position vector, and the particle velocity is rω. Also, it is a scalar equation since only rotation about the z-direction (perpendicular to the screen) is being considered. The equation can be integrated to give, Thus, the sum of the moments about an axis L passing through the center of gravity of a rigid body equals the product of the moment of inertia about L and the angular acceleration,
|
|||||||
|
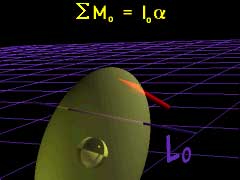
Similarly, the total moment acting on any fixed axis Lo equals the rate of change in angular momentum about Lo, ΣMo = d(Ho)/dt The angular momentum of a rigid body can be expressed in terms of the moment of inertia and the angular velocity, giving Ho = Io ω Further, the sum of the moments about any fixed axis Lo equals the product of the moment of inertia about Lo and the angular acceleration,
|
|||||||