3D Truss Lifting Crate

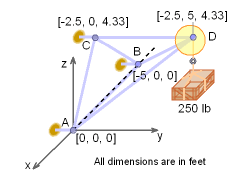
Determine the force in the member CD, BD and AD of the space truss shown in the figure. Note that points A, B and C are in the x-z plane and member CD is parallel to y-axis.

First, the co-ordinates of joints A, B, C and D need to be found.

From the figure it can be seen that  ΔABC is an equilateral triangle with each side of 5 feet. The height of the equilateral triangle will be equal to 5 cos30^o, or 4.330 feet. Thus, the coordinates each joint will be,

     A = [0, 0, 0]               B = [-5, 0, 0]

     C = [-2.5, 0, 4.33]     D = [-2.5, 5, 4.33]

Since, there are only three unknown forces at joint D, the force analysis of the truss will begin at joint D. Recall, with 3D trusses, three equations can be used at each joint.

Let the force in member AD, BD and CD be labeled as F_AD, F_BD and F_CD respectively. Expressing each force acting at joint D in the vector notation gives,

     W = -250 k
     F_AD = F_AD (-2.5i + 5 j + 4.33k) / 7.071
     F_BD = F_BD (2.5i + 5j + 4.33k) / 7.071
     F_CD = F_CD 5j / 5

All forces have to be in equilibrium, giving

     ΣF = 0
     W + F_AD + F_BD + F_CD = 0

Equating the i, j and k components gives,

     ΣF_x = 0
    0.3536 F_BD  - 0.3536 F_AD = 0
    F_BD =  F_AD

     ΣF_z = 0
     0.6124 F_AD + 0.6124 F_BD - 250 = 0
     By substituting F_AD = F_BD
     0.6124 F_AD + 0.6124 F_AD - 250 = 0
     F_AD = 204.1 lb = F_BD

     ΣF_y = 0
     0.7071 F_AD + 0.7071 F_BD + F_CD = 0
     F_CD = -288.6 lb

Members AD and BD are in tension and member CD is in compression.