| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Rotation about a Fixed plane | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
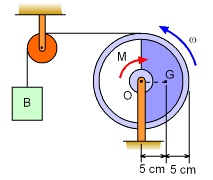 Rotating Wheel with Counter Weight |
Example |
|
|
The unbalanced wheel O has a mass of 30 kg and is connected to a 20 kg counter weight block, B, with a continuous cable. If a constant moment of 15 N-m is a applied to the wheel in the clockwise direction, what is the force exerted on the wheel by the pin at center point, O? At the instance shown, the angular velocity, ω, is 4 rad/s. The center of mass, G is 5 cm from the center and the wheel's radius of gyration is 7 cm (about center point O). Assume the pulley is mass-less and frictionless. |
||
| Solution |
||
|
|
There are two objects that are connected with the cable. Since the pulley is assumed mass-less, the tension in the cable does not vary. The vertical equation of motion for the block is |
|
 Free Body Diagrams with Accelerations |
Find the angular equation of motion for the wheel by summing all forces about O. Note, the wheel weight acts through the wheel's center of mass, and the moment of inertia, I, is related to the radius of gyration, k (I = mk2). Equating the moments to the angular acceleration gives, There are three unknowns, T, α and aBy but only two equations. However, the angular velocity of the wheel and linear acceleration of the block are related, Combining all equations gives, Now that all forces are known, the vertical and horizontal forces on the wheel can be summed, Vertical forces, Total reaction force at the center, O = 340.4 N |
|