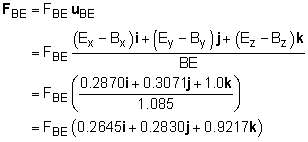Loading

Top View at Point B

FBD of Joint B

Example of Space Truss

Since all members are symmetrical around the inter-stage structure, all members will have the same load. Using the method of joints, the forces at joint B on the bottom ring is analyzed by summing the forces,

     ΣF_B = 0

The free-body diagram includes the external thrust load and all member forces acting at joint B. Since Joint B is in static equilibrium, the summation of all force vectors must equal zero. Since this is a 3D problem, all forces will be represented in the vector i, j, k format.

The total thrust load of 2,400 kN is evenly distributed around the inter-stage structure so each joint will have to withstand a vertical load of 300 kN.

     F_T = 300 k

Truss Diagram

Use the location of points B and E to define the unit directional vector of F_BE.

     E_x = 0.75 sin22.5 = 0.2870 m
     E_y = -0.75 cos22.5 = -0.6929 m
     E_z = 1.0 m

     B_x = 0 m
     B_y = -1 m
     B_z = 0 m

The length of member BE is

     BE = ((0.2870 - 0)² + (-0.6929 - (-1))²
                            + (1 - 0)² )^0.5
          = 1.085 m

The vector F_BE in i, j, k format is

The member force F_BD is similar to F_BE except the x component is reversed. The magnitudes will be the same:

     F_BD = F_BE (-0.2645i + 0.2830j + 0.9217k)

If forces are summed in the z direction, ΣF_z = 0, only one unknown remains, F_BE. Solving for F_BE gives

     2 F_BE 0.9217 + 300 = 0

     F_BE = -162.7 kN   compression