| Ch 6. Modeling and Similitude | Multimedia Engineering Fluids | ||||||
|
Dimensional Analysis |
Similitude |
Dimensionless Groups |
|||||
| Common Dimensionless Groups | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
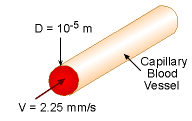
The Reynolds number is given by Re = ρVL/μ where L is the characteristic length. It is assumed that the blood vessel is not collapsible, which means the vessel wall is not deformable, and the stenosis scenario (i.e., constriction or narrowing of coronary vessels due to the buildup of fat and cholesterol) is not considered. Since the blood vessel maintains the circular cross section, the diameter (D) is chosen as the characteristic length, which is 10-5 m. At body temperature, the density (ρ) and viscosity (μ) of the plasma is given as 980 kg/m3 and 0.0014 N-s/m2, respectively. Since the plasma consists 90% of water, the density and viscosity of plasma are close to thase of water (ρ = 999 kg/m3 and μ = 0.0011 N-s/m2). The Reynolds number is calculated to be Re = (980)(2.25)(10-3)(10-5)/(0.0014) Based on the pipe flow model, the calculated Reynolds number is less than 2,100, hence the flow is laminar. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.