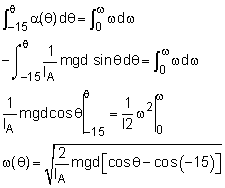| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Rotation about a Fixed plane | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Problem Diagram |
Let the acceleration of the center of gravity of the pendulum be acg = axi + ayj For simplicity, the FBD and MAD are combined into one diagram. The origin of the x-y axis is placed at the pin support, and the reaction forces of the pin support are labeled. Newton's Second Law can be used to sum the forces in both directions, giving ΣFx = Ax = max ΣFy = Ay - mg = may |
|
| Angular Acceleration |
||
|
The angular acceleration, α, is assumed to go in the counterclockwise direction (if wrong it will be negative). The angular acceleration is the same around any point since the α vector actually points directly out of the screen. Summing the moments about A gives ΣMA = IA α -mgd sinθ = IA α or For θ = 0, which is the position requested by the problem, angular acceleration becomes simply α(0) = (-1/7.289) (3.17) (32.2) (1.442) sin0 = 0 |
||
| Reaction Forces |
||
|
The two force equation (Fx and Fy) can be used to find the forces Ax and Ay, but first the acceleration of the center of gravity axi and ayj need to be determined. The acceleration of the center of gravity of the pendulum can be expressed in terms of the acceleration of the pivot point A as acg = aA + α × rcg/A - ω2r = axi + ayj Because point A is pinned, its acceleration is zero, aA = 0 Recall, α(0) = 0, which reduces the equation to acg-θ=0 => -ω2r = axi + ayj To this equation, the angular velocity ω when θ = 0 needs to be determined. Recall that which can be integrated to find an expression for ω giving For θ = 0, the angular velocity becomes ω(0) = 1.173 rad/s |
||
 Relationship Between the Moment and Acceleration |
Substituting gives, acg-θ=0 = -(1.173)2 (-1.442)j = 1.984j ft/s2 = axi + ayj Equate like terms, ax-θ=0 = 0 ay-θ=0 = 1.984 ft/s2 Substitute back into the initial force equations, Fx = Ax = max Ax-θ=0 = 0 Ay-θ=0 = m (ay + g) = 3.17 (1.984 + 32.2) = 108.4 lb |
|