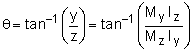| Ch 6. Advanced Beams | Multimedia Engineering Mechanics | ||||||
|
Composite Beams |
Unsymmetric Bending |
||||||
| Unsymmetric Bending | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
| Introduction |
|||||
|
|
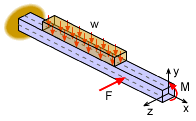
Unsymmetric beam bending is really just two problems added together using the principle of superposition. Normally, a beam is loaded in the y-direction causing a moment about the z axis. But the beam can also be loaded in the z-direction causing a moment about the y axis. Both y- and z-directions are perpendicular to the beam as shown in the diagram. Each direction can be solved separately for bending stress, and then add the results together. If the load is at an angle to the beam, but is in the y-z plane, then the load can be reduced into two forces in the direction of the y and z axes. In this section, all loads are assumed to act through the beam shear center (generally the centroid) so that there is no rotation or twisting about the x-axes. This helps simplify the calculations. |
||||
|
|
Unsymmetric Beam Bending |
||||
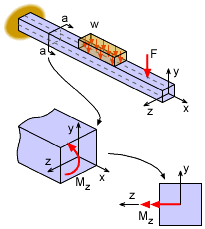 Bending Loading in y-direction Produces Moment About z axis |
First, consider a beam that is loaded only in the y-direction as shown at the left. These loads cause a bending moment about the z axes. This has been analyzed previously in the Bending Stress section. At any given location a-a, the bending stress will be where Mz is the internal moment and Iz is the moment of inertia, both about the z axis. Notice that a positive y produces a negative stress which indicates a compression stress. Also, the double-headed arrow represents a moment rotating about the vector direction. Using the right-hand rule, the thumb points in the direction of the double-headed arrow and the fingers are in the direction of the moment. |
||||
|
|
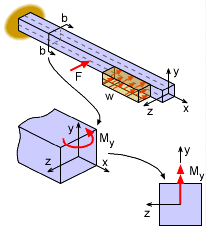
Similarly, loads in the z-direction will cause a moment about the y axes as shown at the left. The bending stress is where My is the internal moment and Iy is the moment of inertia, both about the y axis. The equation does not have a negative sign since a positive z value will produce a positive tension stress. Again, the double headed arrow is a convenient method to represent a moment vector when drawing in 2D. The moment rotates about the direction of the double-headed arrow. |
||||
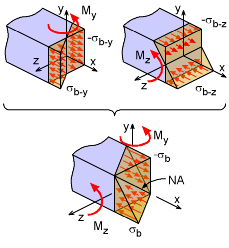 Unsymmetric Bending Stress is the Total of the Bending Stress about the z and y axis |
The two bending stresses, σb-z and σb-y can be added together using the principle of superposition. This gives the final unsymmetric bending stress as
The maximum tension and compression bending stress is not obvious. As shown in the diagram at the left, the bending stress is a tetrahedral shape and increases as the distance from the neutral increases. The neutral axis in not horizontal but is rotated depending on the ratio of the moments, My and Mz, and the moment of inertias, Iy and Iz. More details about the NA is given in the next section below. |
||||
| Neutral Axis (NA) |
|||||
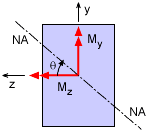 Neutral Axis Rotation Angle |
It is helpful in understanding the bending stress if the location of the neutral axis is known, especially for unsymmetric bending, The definition of the NA is where the bending stress is zero. Thus, if the unsymmetric bending stress equation is forced to equal zero, the result will be the line equation for the NA, or This is an equation for a line that goes through the origin. The maximum bending stress is located at the point which is furthest from the neutral axis (perpendicular direction). The angle between the NA and the z axis is |
||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.