| Ch 6. Modeling and Similitude | Multimedia Engineering Fluids | ||||||
|
Dimensional Analysis |
Similitude |
Dimensionless Groups |
|||||
| Similitude | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
In the Dimensional Analysis section, methods to identify dimensionless parameters governing a particular model were presented. The discussion in this section is focused on how to relate a model to an actual prototype (i.e., the real full scale structure). In other words, it is desired to find out under what conditions will testing or experiments done on a model accurately represent or predict the actual phenomena. |
||
| Similitude |
||
|
|
In the study of fluid mechanics, models are frequently used for testing and development purposes in laboratories before a full scale prototype is built. The model can be either smaller than the prototype (e.g., design of dam, airplane and automobiles) or larger than the prototype (e.g., study of interaction between red blood cells and the vessel wall). Take the aircraft industry for example. It is a common practice to design and develop an aircraft by testing the model in a wind tunnel. This way, the expenses of product development will be reduced considerably compared to conducting the design and development process on a full scale aircraft. The next question would be under what conditions will the model accurately portray the actual full scale prototype. In order to yield useful information from the model being tested, the model and prototype should fulfill the requirement of geometric, kinematic and dynamic similitude, as discussed in the subsequent paragraphs. Geometric Similitude |
|
| An Example: Flow Past a Sphere |
||
|
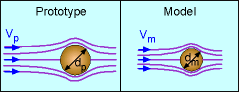
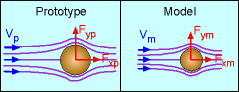
Take flow past a sphere for example. A prototype and model satisfying geometric similitude are shown in the figure. The diameters of the spheres are proportional. Based on dimensional analysis, it can be determined that the drag force (D) can be modeled as, D/(d2ρV2) = function (Re) where Re is the Reynolds number, and is given by Re = ρVd/μ Both the model and prototype should follow the same relationship. In order to satisfy the dynamic similitude requirement, the Reynolds number and dimensionless drag for the model and prototype should be the same: Rem = Rep and Dm/(dm2 ρmVm2) = Dp/(dp2 ρpVp2) where the subscripts m and p refer to the model and prototype, respectively. From this example, it is shown that for the model and prototype to fulfill the requirement of similitude, all the corresponding pi terms should be equal. In other applications, the Froude number will be the same for both the model and prototype when free surface flow is involved. The Weber number will be the same for model and prototype when surface tension force is important. |
|