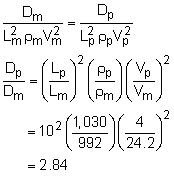| Ch 6. Modeling and Similitude | Multimedia Engineering Fluids | ||||||
|
Dimensional Analysis |
Similitude |
Dimensionless Groups |
|||||
| Similitude | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
The submarine model is built with a scale of 1:10. That is, Lp/Lm = 10 Since submarines usually cruise well below the water surface, the Froude number is not important in this study. In addition, it is assumed that the compressibility effects are negligible, hence the Mach number has no role in this study as well. In order for dynamic similitude, both the Reynolds number and dimensionless drag should be identical for the model and prototype. The Reynolds number for the prototype is calculated as Rep = ρpVpLp/μp = (1,030)(4)(10Lm)/(1.2)(10-3) = 34.3×106 Lm From the properties table of water, the viscosity and density of fresh water at a temperature of 40oC are 0.7×10-3 N-s/m2 and 992 kg/m3, respectively. Equate the Reynolds number for the prototype and model and rearrange terms to yield an expression for the model's velocity Rem = Rep Now, equating the dimensionless drag force for the prototype and model yields In this problem, it was assumed that both the Re and dimensionless drag force relationship where known. They could have been derived using the Buckingham Pi Theorem. |
|
 An
Attack Submarine
An
Attack Submarine