| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Translational Motion | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
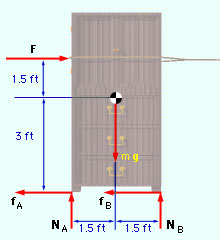 Free-Body Diagram
|
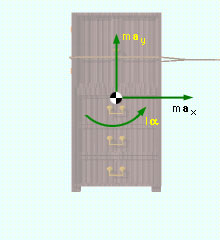
The first issue that needs to be addressed is the unknown reactions at the floor. To determine these, begin with a free-body diagram as shown at the left. Summing the forces in the x and y direction and summing the moments about the center, gives ΣFx = F - fA - fB = max ΣFy = NA - NB - mg = 0 ΣMcg = 1.5NB - 1.5NA - 1.5F - 3fA - 3fB = 0 Noting that fA = μ NA fB = μ NB The y-direction force equation and moment equation can be solved simultaneously for the normal forces NA and NB (the algebra has been omitted): NA = mg (0.5 - μ) - 0.5F NB = mg (0.5 + μ) + 0.5F Noting that m = W/g = 200/32.2 = 6.211 slugs the final reaction become NA = 6.211 (32.2) (0.5 - 0.3) - 0.5 (75) NB = 6.211 (32.2) (0.5 + 0.3) + 0.5 (75) The acceleration of the wardrobe can now be determined using the x-direction force equation, giving ax = 1/m (F - fA - fB) = 1/m (F - μ NA - μ NB) = 1/6.211 [75 - 0.3 (2.5) - 0.3 (197.5)] = 2.415 ft/s2 |
|
| Solution of b) |
||
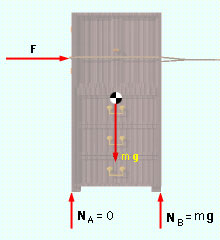 Tipping Diagram |
When the force F is just large enough to cause the wardrobe to tip, the normal force on the left leg is zero, and the right leg supports the entire weight of the wardrobe. Substituting NA = 0 and NB = mg into moment equation, and rearranging gives, ΣMcg = 1.5NB - 1.5NA - 1.5F - 3fA - 3fB = 0 1.5 mg - 1.5 (0) - 3 μ NA - 3 μ NB = 1.5 F 1.5 mg - 3 μ mg = 1.5 F Solving for the minimum force required to tip the wardrobe gives Fmin = mg (1 - 2μ) = 6.211 (32.2) [1 - 2(0.3)] = 80.0 lb |
|