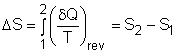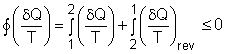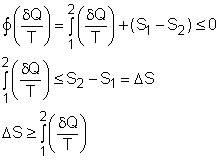| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Entropy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||
| Clausius Inequality
|
|||
The
second law of thermodynamics is developed for systems undergoing cycles
while exchanging heat with two reservoirs. One corollary of
the second law is known as the Clausius inequality, which states that
the cyclic integral of where The Clausius inequality is valid for all cycles, reversible or irreversible. |
|||
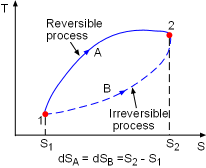
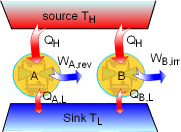 Demonstration of the Clausius Inequality |
To demonstrate the Clausius inequality, consider two heat engines that work between the same two reservoirs. Heat engine A is an reversible heat engine and heat engine B is an irreversible one. Both of these two engines absorb heat QH from a heat source, which has a temperature of TH and reject heat to a heat sink at temperature TL. Applying the first law to both of the engines gives, WA,rev = QH - QA,L WB,irr = QH - QB,L Since a reversible engine has the highest efficiency of any heat engines working between the same source and sink, a reversible heat engine produces more work than an irreversible heat engine for the same heat input QH. WA,rev = QH - QA,L > WB,irr = QH - QB,L QA,L < QB,L Since the temperature TH is constant during the heat transfer
QH, and the temperature TL is constant during the
heat transfer QA,L and QB,L, the cyclic integral
of Comparing the above two equations with QA,L < QB,L yields, A reversible heat engine holds the following relation: Combining the above equation with equation (1) gives, To summarize the above analysis, the Clausius inequality states |
||
| Entropy
|
From the discussion above, , the Clausius inequality states, for an internally reversible cycle The cyclic integral of The entropy change for process1-2 can be determined as |
||
|
|
Note that the above definition actually defines the change of entropy, instead of entropy itself. Because entropy is a property, the entropy change between two specified states is the same whether the process is reversible or not. The previous discussion only means that entropy is a useful property in the second law analysis of an engineering device. But what is entropy? Entropy can be viewed as a measure of molecular disorder. In other words, entropy is the amount of disorder in a system. A pure substance at absolute zero temperature is in perfect order, and its entropy is zero. This is the third law of thermodynamics.
If the substance is not a pure crystal like substance, its entropy at absolute zero is not zero. When the molecular disorder is produced, the ability of doing work is reduced. |
||
| The Increase of Entropy Principle
|
|||
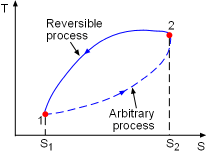
|
|
Consider a cycle as described in the diagram at the left. Peocess1-2 is an arbitrary (reversible or irreversible) process, Process 2-1 is an internally reversible process. From the Clausius inequality, where the equality holds for internally reversible process and inequality holds for irreversible process. |
||
For an isolated system, the heat transfer at the system boundary is zero. The above equation becomes ΔSisolated This equation is known as the increase of entropy principle. It states
|
|||
 Negative Entropy Change of a System |
Entropy is an extensive property, and thus the total entropy of a system is equal to the sum of the entropies of all parts of the system. The combination of a system and its surroundings is an isolated system. For this case, the increase of entropy principle is ΔSisolated = ΔSsys + ΔSsurr The entropy change of a system can be negative. But the entropy change of an isolated system formed by this system and its surroundings can not be negative. The second law of thermodynamics states that processes can occur only in a certain direction. But which direction? The increase of entropy principle answers this question: a process must proceed in the direction that complies with the increase of entropy principle. A process that violates this principle is impossible. |
||