In this section, a method called dimensional analysis along with the Buckingham Pi theorem will be introduced to identify the important dimensionless parameters governing a particular problem.

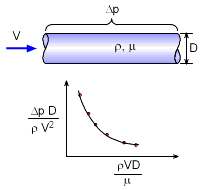
Since analytical solutions are not available for the majority of real fluids problems, experimental work plays a vital role in the study of fluid mechanics. Before setting up an experiment, it is important to identify all dimensionless parameters that govern a system or problem, and ultimately obtain a correlation to relate those parameters. Dimensional analysis is one such method that can be used to minimize the time and expenses spent on experiments and yet obtain valuable information from the fewest number of experiments possible.

To better understand the need for dimensional analysis, consider flow through a simple pipe. As one might imagine, pressure is critical to pipe flow. But how is the change in pressure related to the pipe and liquid? What pipe parameters effects pressure changes in a pipe? Some obvious parameters are velocity, density, pipe diameter, and viscosity. To isolate and test for each of these parameters independently with an experiment may be impossible. Besides, the number of experiments would be vast.

To minimize the experimental effort, the dependent variables are group together to form dimensionless parameters that can be used for other similar pipes. While simple, this is a important tool in developing models for fluid dynamics. An example of five factors that influence pipe flow is shown in the diagram on the left. Two possible dimensionless parameters are plotted, using experimental data points.

Step 1: The first step of dimensional analysis is to identify all independent parameters for the system or study. These parameters generally include fluid properties (e.g., density, viscosity and surface tension), system geometry (e.g., length, area and volume) or flow conditions (e.g., velocity, pressure change and applied force).

Step 2: The second step is to determine the number of basic dimensions involved. Two sets of basic dimensions can be used:
     (i) Force (F), Length (L) and Time (T)
     (ii) Mass (M), Length (L) and Time (T)
For example, the basic dimensions for density can be expressed in terms of FL^-4T ² or ML^-3. Some of the basic dimensions for common parameters encountered in fluid mechanics problems are summarized in the table. Temperature (T) and charge (q) dimensions can be added when considering heat transfer and electrical problems, respectively.

Step 3: The next step is to determine the number of dimensionless parameters (pi terms, denoted by Π) through the Buckingham pi theorem. According to the Buckingham pi theorem, the number of pi terms is equal to (n-k) where n is the number of independent parameters involved (determined in step 1) and k is the number of basic dimensions involved (determined in step 2). Hence, for a given system, one can write

     Π₁ = function (Π₂, Π₃, ..., Π_n-k)

Step 4: From the list of parameters determined in step 1, select k number of repeating parameters. These repeating parameters must include all the basic dimensions, but they cannot be dimensionless or have the same basic dimensions (i.e., do not include both L (length) and L³ (volume) as repeating parameters). In other words, the repeating parameters cannot form dimensionless parameters by themselves.

The pi terms are then formed by multiplying the remaining parameters with the repeating parameters raised to a certain power. The exponents of the repeating parameters are determined such that the pi terms are dimensionless. Once the pi terms are determined, this concludes the dimensional analysis. Experiments can then be conducted to find a correlation among the pi terms.

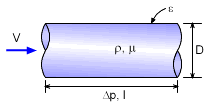
For a better illustration of the use of dimensional analysis, take fluid flow in a circular pipe.

Step 1: The parameters that are involved in the pipe flow problem are the pressure drop (Δp), pipe length (l), pipe diameter (D), fluid velocity (V), fluid density (ρ), fluid viscosity (μ) and pipe surface roughness (ε). A total of 7 parameters (n = 7) is involved in this problem.

Step 2: The basic dimensions involved are summarized in the table on the left. All three of the basic dimensions, M, L, and T (k = 3) are involved in this problem.

Step 3: According to the Buckingham pi theorem, the number of pi terms is 4 (n - k = 7 - 3 = 4).

Step 4: The next task is to determine the form of the pi terms. Select the pipe diameter (D), fluid velocity (V) and density (ρ) as the repeating parameters.

The pi terms are then given by:

     Π₁ = ΔpD^a1V^b1ρ^c1
     Π₂ = lD^a2V^b2ρ^c2
     Π₃ = μD^a3V^b3ρ^c3
     Π₄ = εD^a4V^b4ρ^c4

The exponents of the first pi terms are determined as follows:

     Π₁ = ΔpD^a1V^b1ρ^c1 = (ML^-1T^-2)(L)^a1(LT^-1)^b1(ML^-3)^c1
             = M^{(1 + c1)} L^{(-1 + a1 + b1 - 3c1)} T^{(-2 - b1)}

In order for Π₁ to be dimensionless:

     M:     1 + c1 = 0
              c1 = -1

     T:     -2 - b1 = 0
             b1 = -2

     L:     -1 + a1 + b1 -3c1 = 0
             a1 = 3(-1) - (-2) + 1 = 0

Hence, Π₁ is determined to be Δp/ρV².

Since the basic dimension for the pipe length l is L, by inspection, the second pi term is given by (a2 = -1, b2 = 0 and c2 = 0):

     Π₂ = l/D

Similarly, the last pi term is given by (a4 = -1, b4 = 0 and c4 = 0):

     Π₄ = ε/D

The exponents of the third pi terms are determined as follows:

     Π₃ = μD^a3V^b3ρ^c3= (ML^-1T^-1)(L)^a3(LT^-1)^b3(ML^-3)^c3
             = M^{(1 + c3)} L^{(-1 + a3 + b3 - 3c3)} T^{(-1 - b3)}

In order for Π₃ to be dimensionless:

     M:     1 + c3 = 0
              c3 = -1

     T:     -1 - b3 = 0
             b3 = -1

     L:     -1 + a3 + b3 -3c3 = 0
             a3 = 3(-1) - (-1) + 1 = -1

Moody Chart*
Larger Chart Below

[*Reference: Moody, L. F., "Friction Factors for Pipe Flow," Transactions of ASME, Vol. 66, 1944.]

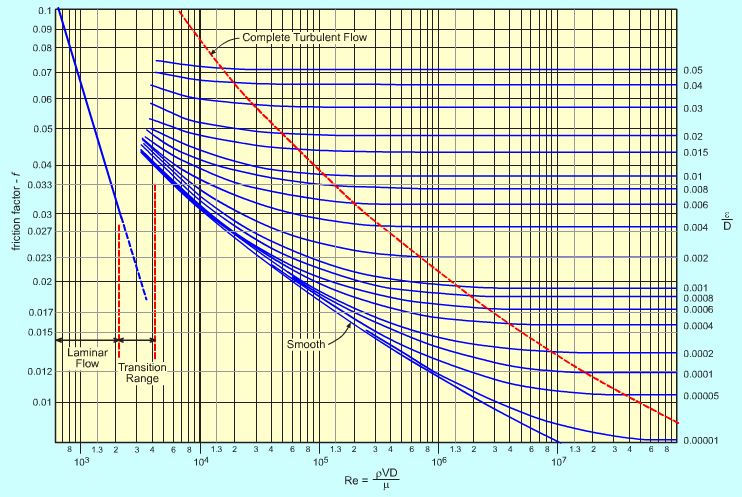
Hence, Π₃ is determined to be μ/ρDV. Recognizing that the inverse of the pi term is also dimensionless, the third pi term can also be written as ρDV/μ, which is the Reynolds number (Re).

For flow in a circular pipe, the pressure drop is then given by

     Δp/ρV² = function(l/D, ε/D, Re)

As is discussed in the Viscous FLow in Pipe section, flow in a circular pipe can be solved with the aid of the Moody chart (obtained from experiments) where the pressure drop term is expressed in terms of the friction factor (f). As shown in the Moody chart, the friction factor is a function of the entrance length (l/D), relative roughness of the pipe (ε/D) and the Reynolds number (Re).